Теория квантовых компьютеров за 30 с лишним лет прошла путь от фантазии к научной догме. В ее основе лежит миф об ЭПР — запутанности, который обсуждался в http://extremal-mechanics.org/archives/12460. Более глубокая статья http://extremal-mechanics.org/archives/16623 подняла вопрос о неполном соответствии теории квантовых компьютеров и квантовой механики, а также волны желчи, на которые я не обращаю внимания. Ни один из «физиков», упражняющихся в заочных оскорблениях, не осмелился вступить в честную дискуссию со мной, для которой сайт «Экстремальная механика» имеет ТЕХнические возможности. При некоторых формальных неточностях, которые присутствуют в научно-популярной статье «Компьютер Бога», в целом ее выводы верны.
Настоящая статья продолжает эту тему. В ней рассмотрен лишь один, но крайне важный аспект. Опыт Алана Аспэ (Aspect) — блестящего экспериментатора и классика квантовой магии, который внес основной вклад в трансформацию ЭПР — мифа в догму. Результаты опытов Аспэ и других были интерпретированы на основе представления о фотонах, как точечных частицах (с обычными оговорками о корпускулярно-волновом дуализме). Оно является ошибочным, т.к. у фотона нет представления Шредингера [2]. Говоря простым языком, для этих частиц понятие пространственных координат лишено смысла. Поэтому нельзя говорить о том, что в определенный момент времени фотон находится в определенном месте. Он может быть локализован в состоянии малого волнового пакета, но в этом случае поляризация теряет смысл. Неявно предполагаемая возможность поляризации точечного фотона легла в основу ложной интерпретации опытов Аспэ. Начнем с краткого описания этих экспериментов (подробности в [1]).
Использовались флуоресцентные источники каскадного излучения, где атомы испускают пары квантов с интервалом нс. В первых опытах один из фотонов пары имел длину волны 551.3 нм (зеленый свет), а другой 422.7 нм (фиолетовый). Считается, что в каждом каскаде фотоны разлетаются в разные стороны, имея одинаковые направления круговой поляризации — левое или правое с вероятностями
, что равносильно пребыванию в суперпозиции двух состояний линейной поляризации в направлениях осей X и Y. Как полагают Аспэ и его последователи, эта пара квантов света рождается в запутанном, поляризационном состоянии. Последнее означает, что если один из фотонов будет обнаружен поляризованным вдоль оси X (для чего достаточно пропустить его через поляризатор с X — ориентацией), то второй автоматически, в то же мгновение окажется в том же состоянии (что можно обнаружить с помощью второго поляризатора). То же самое в отношении оси Y. В этом случае говорят о корреляции между направлениями поляризации фотонов запутанной пары, которую можно измерить.
На схеме пара лазеров возбуждает флуоресцентный источник каскадного излучения, который, по мысли Аспэ, излучает пары запутанных фотонов. Считается, что общее состояние такой пары является запутанным [1]:
(1)
.
Состояния ,
отвечают направлениям поляризации вдоль осей координат, состояния
,
— двум направлениям круговой поляризации кванта
(где
).
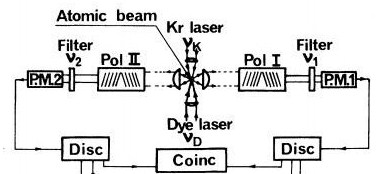
Каждый из фотонов пары проходит через свой поляризатор (Pol I и Pol II), после чего, пройдя через частотный фильтр, попадает в фотоумножитель (PM I и PM II). Последний, по существу, является детектором одиночных фотонов и работает по принципу электронной лавины, которую инициирует фотоэффект. Схема управления фотоумножителями организована так, что каждая пара квантов детектируется во временном окне около 20 нс. Попадание в него случайной пары фотонов от двух разных атомов маловероятно. Малый интервал между срабатываниями счетчика нс служил признаком регистрации пары фотонов от одного атома. Таким образом, схема почти наверняка зафиксирует только пару, излученную в одном каскаде. Происходит это в среднем 100 раз в секунду. Напомним, что каждая такая пара считается ЭПР — запутанной.
Если теперь за некоторый период времени подсчитать числа пар для случаев, когда один из поляризаторов («левый» или «правый») удален, то можно вычислить коэффициент корреляции между событиями поляризованности левого фотона в заданном направлении , а правого в направлении
. Такие измерения позволяют проверить неравенства Белла, а также выявляют корреляцию между поляризациями фотонов каждой пары (для различных направлений
и
). Именно это было сделано группой Аспэ.
Итак, опыты основаны на подсчете фотонных пар, пропущенных через поляризаторы. Однако, вместо этого мог иметь место подсчет одиночных квантов, которые достигали двух фотоумножителей в виде волны со сферическим фронтом.
Для состояния с квантовыми числами и
, отвечающими оператору момента
, собственная функция
линейно выражается через векторные поля
, которые задают два направления круговой поляризации при каждом
[4]. При этом
. Для электродипольного излучения при
и
(опыт Аспэ), согласно (16,23) [4]
(2)
где (в релятивистской системе единиц),
, орты
,
ортогональны между собой и вектору
(см. (16,21) [4]).
Тогда электрическая компонента поля единичного фотона определяется из уравнения
(3)
Из (7,4) [4] следует, что . С учетом этого из (2) получаем:
В силу (16,10) [4] справедливо , где
и
. Отсюда:
(4)
В опытах Аспэ запутанными считались пары фотонов, движущихся в противоположных направлениях. Каждый из двух поляризаторов пропускает через себя часть волны (2), которую можно приближенно считать плоской (3):
(5)
где знаки отвечают двум противоположным направлениям из точки излучения на поляризаторы,
— площадь малого сегмента сферы
вокруг точки
, вещественные константы
и
определяются в силу (2).
В силу (3) волновые поверхности фотона являются сферами . Из (4) и (5) видно, что эта волна приходит к каждому из двух поляризаторов в одинаковых фазах, хотя и в разные моменты времени в силу различной удаленности от излучателя. При этом угол между вектором
и осью каждого поляризатора один и тот же для любой волновой поверхности. Поэтому обе волны (5) взаимодействуют с поляризаторами одинаково, будучи «сегментами» волны фотона. Это и создает иллюзию пары частиц, запутанных в поляризациях. Вернемся в гауссову систему единиц.
На сказанное выше можно возразить, что счетчик фотонов срабатывает дважды в среднем через нс, как и должно быть при излучении каскадов. Однако, время срабатывания фотоумножителя элементарно оценивается
нс. В течение этого времени может быть зафиксирован только один фотон. В действительности он является волновым пакетом, который вблизи сферы
описывается волной (3). Если размер пакета
м, что отвечает допплеровскому уширению спектральной линии
, то время прохождения через фотоумножитель имеет порядок интервала между фотонами одного каскада. В условиях опытов Аспэ такое уширение было возможно. Таким образом, до срабатывания пары фотоумножителей на первом фотоне второй не мог быть детектирован, а к моменту, когда оба устройства готовы принять второй фотон, его пакет уже прошел. По-видимому, в большинстве случаев пара фотоумножителей фиксировала только один из двух фотонов каждого каскада.
Заметим также, что в рассматриваемом состоянии направление движения фотона не определено. Это видно из (3), а также связано с тем, что импульс и его момент не коммутируют. Следовательно, аналогии с классической механикой, которые используются в качестве причины состояния (1), здесь неуместны. Кроме того, излучение фотона сопровождается возмущением. После него атом окажется не в состоянии с нулевым моментом, а в суперпозиции собственных состояний момента. Таким образом, законы сохранения не влекут состояние (1) для пары фотонов одного каскада. За время излучения расстояние между ними составит м. Идея о том, что такая пара рождается запутанной, противоречит здравому смыслу. Впрочем, последнее относится ко всей квантовой магии.
Таким образом, результаты опытов Аспэ имеют интерпретацию, которая не связана с ЭПР — запутанностью. Необходимы более точные оценки, но уже есть основания полагать, что в этих экспериментах совместные состояния (1) не наблюдались. Вместо этого имела место регистрация одиночных фотонов, проходящих сразу через два поляризатора. По-видимому, подобным образом можно объяснить все опыты с т.н. запутанными фотонами [5].
ЭПР — запутанность критически важна для квантовых вычислений. Это понятие является теоретической основой для управления отдельными кубитами и организации параллелизма. Свидетельствами запутанности взаимно удаленных частиц считаются нарушения неравенств Белла. Такие нарушения действительно наблюдаются, но в действительности это означает лишь одно из двух:
a) у квантовых систем нет скрытых параметров, что отвечает квантовой механике и не связано с запутанностью;
b) cкрытые параметры существуют, поэтому измерения одной частицы могут влиять на удаленную другую.
Разумно предположить, что нарушения неравенств Белла влекут за собой a), т.е., квантовая механика не нуждается в скрытых параметрах. Однако, принято считать эти нарушения свидетельствами ЭПР — запутанности фотонных пар. Данная парадигма сформировалась под влиянием работ Аспэ и других ученых, поставивших аналогичные эксперименты. Помимо несомненных нарушений неравенств Белла, в них якобы наблюдались корреляции между направлениями поляризации взаимно удаленных фотонов. Будь это так, для опытной проверки ЭПР — запутанности в неравенствах Белла не было бы необходимости. Стоит заметить, что сам Аспэ, судя по статье х [1], считал свидетельством запутанности только корреляции. По-видимому, в действительности наблюдалась «корреляция» каждого фотона, попавшего в фотоумножитель, с самим собой. Точнее: он достигал двух фотоумножителей почти одновременно.
В связи со всем этим полезно процитировать Дирака [2] (стр. 25):
«… Пусть мы имеем пучок света, состоящий из большого числа фотонов, который расщепляется на две компоненты одинаковой интенсивности. Сделав предположение о том, что интенсивность пучка связана с вероятным числом фотонов, мы получили бы, что в каждую из компонент попала бы половина от общего числа фотонов. Если далее эти две компоненты будут интерферировать, то мы должны потребовать, чтобы фотон из одной компоненты мог интерферировать с фотоном в другой компоненте. Иногда эти два фотона уничтожались бы, иногда же они превращались бы в четыре фотона. Это противоречило бы закону сохранения энергии. Новая теория, которая связывает волновую функцию с вероятностями для одного фотона, преодолевает эту трудность, считая, что каждый фотон входит отчасти в каждую из двух компонент. Тогда каждый фотон интерферирует лишь с самим собой. Интерференции между двумя разными фотонами никогда не происходит.»
Аналогичная мысль звучит в цитате из Гейзенберга, которая касается парадокса ЭПР и имеет отношение к интерпретации опытов Аспэ (W. Heisenberg, стр. 34 [3]).
«В связи с этими рассуждениями здесь должно быть указано на мысленный эксперимент, предложенный Эйнштейном. Вообразим один световой квант, который представлен посредством волнового пакета, построенного из максвеллевских волн и которому, таким образом, приписана известная область пространства и, в смысле соотношений неопределенности, также определенная область частот. Посредством отражения от полупрозрачной пластинки мы можем очевидно легко разложить этот волновой пакет на две части: отраженную и прошедшую. Тогда существует определенная вероятность найти световой квант или в одной, или в другой части волнового пакета. Через достаточно долгое время обе части будут сколько угодно далеко удалены друг от друга. Если теперь посредством опыта будет установлено, что световой квант находится, положим, в отраженной части волнового пакета, то это одновременно даст, что вероятность нахождения светового кванта в другой части равна нулю. Опыт на месте отраженной половины пакета производит тем самым некоторое действие (сведение волнового пакета!) на сколь угодно удаленном расстоянии, где находится другая половина, и легко видеть, что это действие распространяется со сверхсветовой скоростью.»
Таким образом, попытки обнаружить ЭПР — запутанные пары фотонов с помощью интерферометров лишены смысла. Допустим, мы разделили световой луч полупрозрачным зеркалом, после чего пропустили один пучок через поляризатор. Согласно парадигме ЭПР, возникают запутанные пары одинаково поляризованных фотонов из двух пучков. Это может быть проверено через интерференцию, но так как интерферировать каждый фотон будет с самим собой, совпадение измеренных в разных местах поляризаций не может быть истолковано, как ЭПР — запутанность.
Представления о запутанных состояниях взаимно удаленных частиц, восходящие к парадоксу ЭПР, широко популяризованы и уже считаются частью квантовой механики. Одной из целей данной статьи было показать, что фундамента под этим нет. Мыльный пузырь на иллюстрации символизирует волновой фронт фотона с заданным угловым моментом, а также теорию квантовых компьютеров, основанную на ЭПР — запутанности.
Ссылки:
1. A. Aspect. Bell’s theorem: the naive view of an experimentalist, in Quantum [Un]speakables — From Bell to Quantum information, 2002, R. A. Bertlmann and A. Zeilinger, Springer, http://www.chronos.msu.ru/old/RREPORTS/aspek_teorema_bella.pdf
2. П.А.М. Дирак. Принципы квантовой механики, 1960, Москва: Физматгиз (перевод английского издания P.A.M. Dirac. The principles of quantum mechanics, 1958, Oxford: Clarendon press), 1932).
3. В. Гейзенберг. Физические принципы квантовой теории, Москва: ГТТИ (перевод немецкого издания W. Heisenberg: Die Physikalischen Prinzipien der Quantentheorie, 1930, Leipzig).
4. В.Б. Берестецкий, Е.М. Лифшиц, Л.П. Питаевский. Квантовая электродинамика, Москва: Наука, 1989.
5. T. Inagaki, N. Matsuda, O. Tadanaga, M. Asobe, H. Takesue. Entanglement distribution over 300 km of fiber // Optics Express, v. 21, Issue 20, pp. 23241 — 23249 (2013).
Подробная, строго научная статья об опыте Аспэ и понятии запутанности: http://extremal-mechanics.org/wp-content/uploads/2017/02/Article_Z.pdf.
Дмитрий Зотьев



Несколько странно, что у этой статьи крайне мало просмотров. А ведь ее материал является сенсационным! Он выбивает экспериментальную опору из-под мифа об ЭПР-запутанности и всей теории квантовых компьютеров, основанной на нем.
А что Вы не хотите провести свои опыты, изготовить приборы (пусть с привлечением сторонних сил и финансов), выступить на научном конгрессе? За идею надо бороться и может Вы впишете и своё имя в истори науки!
Так что, это очередной флогистон?
Смотря о чем Вы пишите. Если квантовая магия, то да. Но я бы не стал сравнивать это с флогистоном. Скорее философский камень XXI века.
Считаете, что это более высокое заблуждение. Можно и так. Мне с самого начала эти квантовые компьютеры казались совершенно нереальными. Но история с ними всё тянется и тянется…..
Да не то, чтобы высокое. Сказочно многообещающее )) Аналогично, мне с первого взгляда не понравилась концепция ЭПР-запутанности. Было это лет 6 назад.
Бредовая идея, но как сильно она внедрилась в научное сообщество! Умные люди готовы верить в глупости, если они сулят чудесные возможности и привлекают гранты. На эти темы уже написаны сотни, если не тысячи диссертаций. Полагаю, что теперь из-под квантовой магии выбит краеугольный камень — эксперименты Аспэ.
На этом сайте можно поделиться соображениями по поводу «квантовой магии», не опасаясь обвинений в безграмотности и т.п. личностных нападок (при условии взаимно вежливого поведения, конечно). Предметно обсуждать эти темы на других ресурсах почти невозможно — господа титульные физики воспринимают критику ЭПР-запутанности с какой-то болезненной агрессией, а все их аргументы, как правило, сводятся к обвинениям в неграмотности. При этом сами часто несут такую ахинею в стиле журнала «Популярная механика», что удивляешься тому, как низко упал уровень физического образования в стране юристов, экономистов и прочих «эффективных менеджеров»!
Итак, мысли на эту тему приветствуются и не используются в качестве предлога для троллинга. Данный сайт читают не так уж мало людей, стоит заметить, но вот писать решаются не часто. А между тем, здесь есть удобная возможность для записи формул в Latex-е. Что еще нужно для содержательных дискуссий о квантовых компьютерах, которые на большинстве сайтов глушатся спесивыми окриками носителей дипломов физтеха и физфаков? Титульные физики, которые запутались в квантовой механике, заигравшись в квантовую магию, теперь ревностно оберегают мир своих детских фантазий ))
В качестве примера ЭПР — запутанной пары часто приводится пара электронов, освободившихся из атома после его ионизации. Но собственно почему они должны находиться в запутанном по спинам состоянии
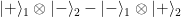 ?
?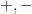 указывают направление проекции спина на ось
указывают направление проекции спина на ось  (допустим). Принято думать, что такая запутанность возникает в силу закона сохранения момента количества движения, если атом до ионизации был в состоянии с нулевым полным моментом, а вызвавший ионизацию квант вовсе не имел углового момента (будучи, например, в состоянии линейной поляризации и собственном состоянии импульса) или же ионизация произошла от удара атома с нулевым моментом.
(допустим). Принято думать, что такая запутанность возникает в силу закона сохранения момента количества движения, если атом до ионизации был в состоянии с нулевым полным моментом, а вызвавший ионизацию квант вовсе не имел углового момента (будучи, например, в состоянии линейной поляризации и собственном состоянии импульса) или же ионизация произошла от удара атома с нулевым моментом.
Здесь 1 и 2 — номера частиц, а знаки
Но в квантовой механике законы сохранения нельзя воспринимать буквально так, как в классической. Электроны находятся в суперпозициях спиновых состояний, где проекции спинов не определены. Банальность в общем-то, но о таких вещах почему-то забывают многие из тех, кто занимается квантовыми компьютерами и поддерживает ЭПР — парадигму.
Разумно предположить, что после вылета из атома пара электронов находится в сепарабельном (и независимом конечно) состоянии
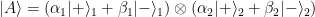 .
.

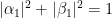 и
и 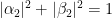 ,
, 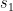 и
и  — операторы спина, а
— операторы спина, а 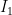 и
и  — тождественные операторы на пространствах состояний электронов по отдельности.
— тождественные операторы на пространствах состояний электронов по отдельности.
Это особенно напрашивается, когда частицы разлетелись «бесконечно далеко». Тогда легко проверить, что среднее значение углового момента данной пары пропорционально числу
где
В силу закона сохранения углового момента должно быть
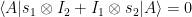
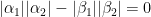 . Таким образом, 4 комплексных числа
. Таким образом, 4 комплексных числа  связаны тремя алгебраическими уравнениями. Следовательно, существует континуум различных сепарабельных состояний этой пары электронов, которые НЕ противоречат закону сохранения углового момента.
связаны тремя алгебраическими уравнениями. Следовательно, существует континуум различных сепарабельных состояний этой пары электронов, которые НЕ противоречат закону сохранения углового момента.
(среднее значение момента пары нулевое), что эквивалентно
Тогда откуда взялось убеждение, что данная пара должна находиться в запутанном состоянии
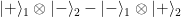 ?
?
Из слишком горячего желания сделать былью сказку об ЭПР — запутанности ?.
А какое тензорное будет, если еще и переставить частицы местами?
Тензорные сомножители переставляются согласно перестановкам частиц.
Считается, что в каждом каскаде фотоны разлетаются в разные стороны, имея одинаковые направления круговой поляризации — левое или правое с вероятностями 0.5, что равносильно пребыванию в суперпозиции двух состояний линейной поляризации в направлениях осей X и Y.
Откуда X,Y — R>+L> даст только одну линейную, или это уже относительно поляризатора?
И ысчо, разве взаимодействие с фильтром не должно сколлапсировать состояние пары развязать
частицы (альтернативного пути же нет- либо проходит, либо поглощается) еще до поляризатора?
Ну и проблема с настройкой окон- прямо в духе КМ- «лишние знания», это уже не токмо неприятности по-Хренникову.
А значит, результат- по-Беллу, то-есть — статистическая корреляция.
Первый вопрос не понял. Какую «одну линейную»?
Насчет второго … Даже размышлять об этом не хочу, поскольку совместных (т.е. запутанных) состояний взаимно удаленных частиц не существует. С парой фильтров взаимодейсвует один фотон. Об этом собственно статья ))
По Беллу есть только неравенство, которое действительно нарушается. Но это не означает наличия корреляций.
«Но в действительности наблюдалась «корреляция» каждого фотона, попавшего в фотоумножитель, с самим собой. Точнее — он достигал двух фотоумножителей почти одновременно. Рассмотрим этот вопрос в деталях.»
«Покажем, что это могло быть подсчетом одиночных квантов, которые достигали двух фотоумножителей в виде волны со сферическим фронтом.»(Почему здесь в формулу (1) просто нельзя добавить недостающие перестановочные компоненты совместного тензорного произведения |R2>|R1>+|L2>|L1>?)
-Это что, намек на регистрацию одного и того же фотона одновременно разными умножителями?! Думаю, не должна вообще регистрироваться функциональная корреляция при паралельных поляризаторах! Только статистическая.
«Cледовательно, эллиптическая поляризация является смешанным состоянием. В связи с этим уместно процитировать Дирака.»
-Почему, из цитаты следует прямо противоположное, в эллиптической те же линейные компоненты, что и в круговой, и они интерферируют по-Дираку, а значит это суперпозиция.
Это не намек, а прямое утверждение — главное в статье. Вы бы все-таки разобрались в ней сначала, потому что явно реагируете на отдельные фрагменты.
Дирак тут не при чем. Вы и многие другие, в том числе даже Фейнман, путают суперпозицию э-м волн и суперпозицию состояний фотонов. Две линейно-поляризованных волны интерферируют в эллиптически-поляризованную, да, но фотон в суперпозиции двух состояний линейной поляризации отнюдь не пребывает в состоянии эллиптической поляризации. Опять же, прочтите все-таки статью внимательно и целиком. Иначе мы будем впустую тратить время.
И пожалуйста, не пишите на каждую свою мысль отдельный коментарий. Соберите все в один и дождитесь ответа ))
Да я и попробовал- размер окна се согласен, так что 4 пятых текста стер. Посоветуйте выход.
А насчет регистрации той же частицы в двух умножителях по-подробней, пожалуйста.
Думаю важнее найти ошибку у Аспэ в трактовке ортодоксальной КМ и результата, ну а потом предлагать альтернативу.
Ну и об частой ошибке:- вектор джонса один, что в КМ, что в классике, и смысл тот же. Так что хоть в этом Дирак не ошибся. А |X>+|Y> действительно линейная, и примени Аспэ другой тип поляризатора, не было бы триумфа.
Ответ можно в личку, чтоб не засорять…
Наверное проблема в том, что Вы не зарегистрированы на сайте. Для этого нажмите голубую надпись «Вход» в правой-верхней части главной страницы (справа от заголовка «Экстремальная механика»). Дальше сами все увидите. Формулы можно и желательно писать в LAТЕХе. Для этого нужно написать «$latex» слева от формулы и «$» справа. Кавычки не нужны!
Я не альтернативу предлагаю трактовке опытов Аспэ, а просто утверждаю, что он в этом ошибся, и вся эта бурная деятельность вокруг квантовых компьютеров основана на популярном заблуждении. Дирак, на мой взгляд, ни в чем не ошибался и ошибок в КМ я не вижу. Хотя и понимаю, что при желании придраться можно. Но «ортодоксальная» КМ успешно работает уже 90 лет. На мой взгляд, в наше время более актуальна проблема ее понимания. Люди спешат исправить классиков, не разобравшись как следует в основах ))
Все же давайте короткими выстрелами(заметками), вопрос-ответ, без обтеканий. Ну, если короткие,
то несколько, ну если дискуссия наметилась- на шкапу и в личку, если захотите.
Исправить классиков- сделано, началось: Белл- Нейман, Фейнман- Борн.
Фейнман в своей нобелевской статье описывает как он до такого «докатился». По-Фейнману,- не благодаря, а вопреки КМ. КМ- если и существует, то в зачаточном состоянии.
90-лет (правда без учета изобретения паровоза) успешного угадывания и метода тыка- читайте Аспека, наивного экспериментатора.
А насчет трактовки синглетного состояния как спутанного- так это все после успехов Аспэ. ( как там насчет системки из 4-х уравнений?).
Ну и : Дирак не ошибался когда, до 1940 или после. Как там у Паули- И Дирак прирек её…
Да,- с латексом будут проблемы -формулы со-временем жшчэзають!
Почитайте статью Белла, а не комментарии почитателей Аспэ. Нет там никакого исправления КМ. Фейнман не исправлял, а скорее надстроил КМ. Борн предложил вероятностную интерпретацию волновой функции, насколько помню. Насчет Неймана не могу вспомнить, но не суть (если «скрытые параметры», то спорная интерпретация, как раз нарушения неравенств Белла ее опровергают). Я не изучал историю КМ, но глубоко изучал «ортодоксальную» КМ по Дираку и Гейзенбергу (думаю этого достаточно).
Почитайте книгу Дирака, чтобы не писать о том, что КМ — «успешное угадывание и метод тыка». Скорее это можно отнести к КЭД и то лишь отчасти. «Ортодоксальная» КМ — это красивая и стройная теория. Просто мало, кто потрудился в ней разобраться, прежде чем начинать критиковать. Это касается многих современных физиков и математиков, самоуверенно пишущих на такие темы. Известную работу Аспэ я читал разумеется, т.к. написал эту критическую статью к ней. «Квантовое запутывание» в том виде, как его понимают популяризаторы квантовых компьютеров, телепортации и прочих чудес, является далеко идущей фантазией на тему КМ, а не частью КМ, как нас пытаются убедить. Поэтому критиковать нужно не «ортодоксальную» КМ, а сами эти фантазии.
«Насчет системки из 4-х уравнений» поясняется в статье. В ней нет ни одного символа без объяснения, что именно он обозначает. У меня нет времени и желания дискутировать лишь бы дискутировать. Если Вам есть что возразить к моим тезисам по существу, то пишите конкретно и желательно в ТЕХе, т.к. я не хочу напрягать глаза и мозг, занимаясь дешифровкой. Мои формулы не исчезают со временем. В конце концов, закиньте куда-нибудь текст возражений и опубликуйте здесь ссылку.
Текст статьи подвергся коррекции и, я надеюсь, стал более понятным.
Вы пишете, что «По-видимому, в большинстве случаев пара фотоумножителей фиксировала только один из двух фотонов каждого каскада.»
Насколько я понимаю, это невозможно. Один фотон не может быть зарегистрирован сразу двумя фотоумножителями. Он конечно может (и будет) интерферировать с самим собой, если созданы условия для интерференции (например щели). Но в результате процесса измерения он будет зарегистрирован только одним фотоумножителем.
Фотон с постоянным угловым моментом, а именно такие рассматривались в опытах Аспэ, является сферической волной. Так почему же эта волна не может быть зарегистрирована в двух разных местах (до которых она добралась) ? Говоря «это невозможно» Вы придаете абсолютный, догматический смысл понятию об измерении квантового объекта. А между тем, результаты опытов Аспэ и им подобных как раз и вынуждают нас уточнить эти представления.
Почему бы не допустить, что измерение может осуществляться несколькими приборами, расположенными в разных местах? Так, что энергия кванта делится между этими устройствами. Последнее предположение уязвимо для критики, но ведь точного определения измерительного устройства все равно нет. Просто нужно расширить представление об измерении, что я и предлагаю сделать вместо того, чтобы придумывать сказки о квантовой запутанности в смысле парадокса ЭПР ))
Вы сами указали, что гипотеза о двойном детектировании натыкается на проблему разделения энергии. Если вы не укажите как её решить, вся гипотеза теряет смысл. И вы должны понимать, что выдвигая такие гипотезы, вы идёте против отцов основателей квантовой механики (которых вы цитируете) и фактически предлагаете новую физику. И я бы еще предложил вам, если вы будете настаивать на своей гипотезе, придумать эесперимент, в котором можно было бы подтвердить, что одну частицу можно зарегистрировать двумя детекторами. Если такого эксперимента поставить нельзя (по любым причинам), то ваша гипотеза становится непроверяемой и в попперовском смысле антинаучной. А если можно, нужно ставить эесперимент
Во-первых, я не иду против отцов-основателей КМ! У них ничего такого нет, что придумали Эйнштейн, Подольский и Розен (парадокс ЭПР). Я глубоко изучил основополагающие книги Дирака и Гейзенберга (Дирака читал еще в юности) прежде, чем рассуждать на эту тему. Чего и Вам советую прежде, чем выносить вердикт о моих отношениях с отцами-основателями )) Большинство из тех физиков и математиков, кто сегодня носится с квантовыми чудесами, первоисточников, похоже, не читали. Но при этом уверенно апеллируют к «формализму квантовой механики», как якобы надежной основе их ЭПР — фантазий.
Да, явление запутанности может иметь место в системах из тождественных частиц (например электроны в атоме). Но это не означает, что ЛЮБОЙ формальный набор тождественных частиц является такой квантовой системой (с пространством симметричных или антисимметричных состояний). Адепты квантовой магии утверждают обратное, именно на этом основана идея парадокса ЭПР.
Во-вторых, проблемы разделения энергии нет. Есть сомнения по этому поводу, но они не могут быть сформулированы в виде проблемы. Два детектора поглощают квант целиком вместе с его энергией. В чем здесь проблема? Что два детектора — это не один? А если их сдвинуть близко, то в чем будет принципиальная разница с одним детектором? Только в локализации квантового объекта в момент его измерения! Но в том-то и дело, что фотон НЕ локализован. Он одновременно пребывает всюду, где есть его поле, грубо говоря. Поэтому Вы не можете четко определить, что есть измерительный прибор. А значит и проблемы нет.
Что касается экспериментов, на которых Вы настаиваете, то они УЖЕ были проведены. Это — опыты Аспэ и многих его последователей. Я как раз и предлагаю их интерпретацию, которая не апеллирует к чудесам. На мой взгляд, выводы Аспэ были в корне неверными, хотя сам эксперимент проведен безупречно.
Вообще, Вы бы не торопились лихим наскоком выдавать категорические заключения. Я с удовольствием с Вами подискутирую, если Вы готовы к СОДЕРЖАТЕЛЬНОЙ дискуссии. Если Вам есть, что возразить по существу, то я готов ответить. Но заявления об отцах-основателях и т.п. лирику оставьте пожалуйста популяризаторам и тем «экспертам», кто знаком с квантовой механикой лишь по лекциям в университете и статьям о квантовых компьютерах ))
Вы пишете: «Но в том-то и дело, что фотон НЕ локализован. Он одновременно пребывает всюду, где есть его поле, грубо говоря».
В «классической» квантовой механике предполагается, что частица делокализована только в процессе своего распространения, а в момент взаимодействия с детектором она локализуется в одном конкретном месте, а не делится между детекторами.
Про отцов основателей я вспомнил, потому что с одной стороны вы их цитируете, чтобы указать на неверную интерпретацию эксперимента Аспе, а с другой стороны тут же предлагаете свою интерпретацию, которая также противоречит отцам основателям, как и интерпретация Аспе.
Кроме того, я думаю, что ваша идея несостоятельна по чисто техническим причинам. У ФЭУ есть порог срабатывания. Фотон с энергией меньше определенного уровня не сможет породить электрон в фотокатоде. Поэтому, если фотон одновременно детектируется в двух ФЭУ его энергия должна быть минимум в два раза выше этого порога. Получается, что если ваша гипотеза верна, то результат эксперимента Аспе будет зависеть от спектральной отсечки ФЭУ. Если он использовал длину волны 551 нм, то ФЭУ ему нужно с чуствительностью как минимум на 1102 нм. А если взять ФЭУ с отсечкой, скажем, на 900 нм, то эффект «телепортации», согласно вашей гипотезе, перестанет наблюдаться. Осталось выяснить есть ли такая зависимость в эксперименте.
Я пишу так, как есть. О том же утверждал и Дирак, между прочим.
Частица локализуется не актом измерения. А тем, что волновая функция дает ощутимую плотность вероятности ее пребывания в определенной области пространства. При измерении частица переходит в стационарное состояние измеряемой величины. Если таковая величина есть набор координат, то можно говорить о точечной локализации (в пределах погрешности измерения). Но у фотонов нет координат в принципе, как нет и волновой функции координат (надеюсь Вы знаете об этом, будучи, судя по Вашим заявлениям, глубоко знакомым с трудами отцов-основателей). Поэтому, применительно к фотону, можно говорить лишь о локализации внутри измерительного прибора. Каковым прибором можно считать и пару детекторов.
Хотя вряд ли Вы читали кого-то из отцов-основателей, если так уверенно приписываете им то, чего у них не было («квантовую магию»). Шредингер, разве лишь, рассуждал на тему ЭПР — эффектов. Но ни Бор, ни Гейзенберг, ни Дирак не заявляли о том, что две удаленные частицы могут мистическим образом взаимодействовать через запутанность. Поэтому ссылка на отцов — основателей несостоятельна.
Вот и выясните для начала, «есть ли такая зависимость в эксперименте», прежде чем заявлять, что «ваша идея несостоятельна по чисто техническим причинам». Вы же не знаете, какой была «отсечка» ФЭУ в опытах Аспэ. Так узнайте, чтобы обосновать свои уверенные заявления и перейти наконец к содержательному разговору! Я задумывался над этим вопросом, когда писал статью, но навскидку нужных данных не нашел. Насколько помню, что-то меня в этом плане успокоило.
Пока Вы только пытаетесь срубить мою точку зрения на скаку, начитавшись, как мне кажется, популярных текстов о квантовой запутанности. Хотите серьезного разговора — пожалуйста. Но на такую пикировку мне жаль времени.
Я фактически предложил вам экспериментальный способ проверки вашей гипотезы, а вы меня отсылаете проверять самому… Мне кажется эта проверка нужна больше вам, чем мне.
Кроме того, у вас, похоже, сложилось неверное предубеждение насчёт моего отношения к квантовой телепортации. Вы наверное думаете, что я её сторонник?
Это не так.
Наоборот. Я убеждён, что никакой телепортации не существует и не понимаю, почему вообще вновь возник этот вопрос спустя столько лет после того, как группа Нильса Бора дала детальный ответ на парадокс ЭПР еще в 30-х годах 20 века.
Но и ваша интерпретация, считаю, ошибочна.
Я задумывался над этим вопросом, когда писал статью, но навскидку нужных данных не нашел. Насколько помню, что-то меня в этом плане успокоило. Из общих принципов работы ФЭУ кажется. Сейчас у меня нет времени, чтобы разбираться с этим вопросом. Но Вы же заявляете, что на этом основании моя интерпретация опытов Аспэ ошибочна. Значит Вам и нужно свою точку зрения обосновать. Иначе странно получается: вы что-то предположили, не имея точных данных, а я теперь должен опровергать Ваше предположение, отыскивая эти данные. Нет уж, извините ))
Я в данный момент занят совсем другим, хотя еще вернусь к этой проблеме вскоре. То, что я утверждаю, основано строго на КМ и КЭД. Как теоретика меня это удовлетворяет. Может быть я ошибаюсь, но пока еще никто не предъявил серьезных контр-доводов кроме того, насчет чего я уже высказался с раздражением. Хотя желающих было очень много, в том числе среди физиков и прильнувших к этой секте математиков (последних кажется даже больше). Если Вы не разделяете всеобщее помешательство на квантовой магии, то как Вы объясните опыты Аспэ? На них ведь держится это учение, как христианство на Библии!
Два отдельно работающих независимых макроскопических детектора нельзя рассматривать, как один КМ детектор. С точки зрения КМ это два прибора и два акта измерения. И в каждом регистрируется один фотон, а не половинка фотона.
Их можно рассматривать как один прибор, только если они будут неделимы. Например квантово- связанными, так чтобы нельзя было понять какой именно детектор сработал. Для этого их придётся разместить на очень близком расстоянии друг от друга, фактически слить их в один детектор и сделать им один выход.
В КМ понятие измерительного прибора не определяется, так что не стоит на нее ссылаться всуе. «Очень близкое расстояние друг от друга» не отличается от очень далекого, если речь идет о макроскопических телах и их взаимодействии с субатомным объектом. Вы в сущности снова заявляете о том, что Вам не нравится моя интерпретация опытов Аспэ, не приводя убедительных аргументов и не предлагая свое объяснение. Тогда Вам придется вступить в секту «Свидетелей ЭПР — чуда», т.к. Вы защищаете ее экспериментальную основу. Так как насчет частотной отсечки фотодетекторов в опыте Аспэ, которую Вы приводили в качестве контраргумента? Вот это стало бы действительно серьезным возражением ))
Искать доказательства вашей маргинальной теории нужно вам, а не мне. Я вам предложил способ проверки, но вы им не заинтересовались. Видимо, вы истинный теоретик и такие мелочи, как соответствие ваших гипотез эксперименту вас не волнуют!
Я не буду больше прикладывать усилий, чтобы убеждать вас в том, что вы ошибаетесь. Первый раз, когда речь шла о повороте в невесомости, мне пришлось затратить много усилий, но я вас убедил. Второй раз, когда речь шла о температуре зеркального паруса, где вы неправильно вычисляли температуру, вы отвергли все аргументы и я не стал больше писать. Сейчас, вы откровенно предлагаете маргинальную интерпретацию, но даже не заинтересованы в проверке своих теорий. Это плохо. Искать нужно аргументы против своих теорий, а не за. Тогда теория будет сильной.
У меня нет задачи вас переубеждать. Я только указал на серьёзные просчёты, а дальше вы уж сами.
Успехов!
Да, один раз я согласился с Вами в вопросе о способности космонавта в невесомости изменить свое пространственное положение за счет сложных движений. Но, подумав немного после этого Вашего комментария я понял, что ошибались все-таки Вы. Подробности данного спора в новой версии статьи «Авторотация в пустоте» http://extremal-mechanics.org/archives/25238.
Видимо этот случай раздул Ваше самомнение до такой степени, что Вы заговорили со мной тоном учителя. При этом в случае с зеркалом не я ошибся, а Вы проявили незнание и/или непонимание теории излучения черного тела (закона Стефана-Больцмана). Вы там писали самоуверенную ерунду, не желая даже вникнуть в незнакомую Вам тему http://extremal-mechanics.org/archives/24340.
Теперь Вы с таким же апломбом рассуждаете о квантовой механике, с которой явно знакомы по научно-популярным статьям и/или обрывкам воспоминаний о лекциях, прослушанных и толком не понятых в студенческие годы. Моя теория не является маргинальной потому, что это — не теория. Просто интерпретация опытов Аспэ, отличная от общепринятой, но основанная исключительно на квантовой электродинамике. Ничего альтернативного ей я не предлагаю, поэтому термин «маргинальная» лишь отражает Вашу неспособность выдвинуть содержательный контраргумент.
Неужели Вы думаете, что мне не приходило в голову то, что Вы предлагаете проверять? Разумеется я об этом думал, но точных данных о чувствительности ФЭУ в опытах Аспэ найти не смог. Но помню, что какая-то информация общего плана убедила меня в том, что при вдвое меньшей частоте фотонов фотодетекторы сработали бы и с большим запасом. Теперь заявляетесь Вы и требуете, чтобы я бросил все дела и начал искать точные данные об аппаратуре в опытах Аспэ, тратя деньги на доступ к некоторым публикациям. Лишь потому, что Вам хочется думать, что таким образом Вы сможете меня опровергнуть. Вы же пытаетесь опровергнуть, вот и опровергайте! А мне задания на самопроверку выдавать не нужно.
Обнаружил статью РИА, в которой профессор Юджин Ползик из института Нильса Бора на полном серьёзе рассказывает, как они телепортируют облака частиц с отрицательной массой, а также сумели (внимание!) преодолеть принцип неопределённости Гейзенберга! При этом он между делом сообщает, что придерживается Копенгагенсой интерпретации КМ. Возглавил какой то там совет РКЦ в Сколково.
Это какой то сюрреализм…
https://ria.ru/science/20180520/1520866846.html
В этой фотографии отражена вся суть стиральной машины, разместившейся под крышей фонда Сколково http://extremal-mechanics.org/wp-content/uploads/2018/06/сколково.jpg . Сделана на одном из недавних сборищ, посвященных т.н. цифровой экономике. Понты и распил бюджета умирающей науки — вот, чем они там занимаются. Не случайно сутенер небезызвестной Насти Рыбки (томящейся в Таиландской тюрьме), мошенник по кличке Алекс Лесли был до побега из России резидентом в Сколково. Хотя девушки на фотографии красивые. Жаль только, что без силикона, видимо, одна из них не обошлась.
я не специалист в КМ, но ваша версия очень даже правдоподобна хотя возможно и не до конца проработана. Но почему вы каждый раз оппонентам в качестве аргумента не напоминаете на экспериментально обнаруженную однофотонную интерференцию, где фотон интерферирует сам с собой?
А вот насчёт классической КМ я с вами не согласен. Эта теория является примером чисто математической схоластики под видом физики, когда вначале делается вброс математической формулы, а потом люди сто лет ищут её физическую интерпретацию. И ведь так до сих пор и не нашли. А КМ-нелокальность — это практически откат к дальнодействию. Ну раз уж вы правильно призываете к отказу от всякой мифологии, то может быть сможете построить новую версию КМ, но как физическую, а не математическую вероятностную модель: то есть сначала физический смысл и физическая модель безо всяких математических спекуляций, а потом описание этой модели с помощью математики.
Еще Дирак отмечал, что интерференция только так и происходит — фотон интерферирует с самим собой. Я об этом писал много раз.
Эксперименты с интерференцией одиночных фотонов, если они проводились, лишь подтверждают теоретически понятный и давно известный факт. Он может стать откровением лишь для тех грамотеев, которые носятся с квантовой запутанностью, как дурень с писаной торбой.
Что касается КМ, то ее мало кто толком понимает. Более актуально не опровергать эту глубокую теорию, а изучать ее как следует. Нет там никакой математической схоластики. Схоластикой занимаются математики, которые уверовали в квантовые компьютеры. Какие математические спекуляции, если эта теория блестяще подтверждается экспериментами на протяжении почти 90 лет?! Может быть Вы имеете ввиду интерпретацию КМ, которую предложил фон-Нейман? Но и там неверно говорить о спекуляциях. Он просто пытался навести математическую строгость, которая на самом деле была не нужна. Я даже не хочу обсуждать вопрос о каком-то переделывании КМ Гейзенберга и Дирака. Научный мир, запутавшийся в квантовой запутанности, остро нуждается в ее понимании, а не изменении ))
не отвечать — это ваше право, что правда не может способствовать более полному пониманию ваших идей, но всё равно спасибо за такую наглядную интерпретацию экспериментов по так называемым спутанным состояниям.
Я просто не хочу тратить время на чуждую мне критику КМ. Спасибо и Вам за доброжелательный комментарий.
«Вместо этого имела место регистрация одиночных фотонов, проходящих сразу через два поляризатора.», — при условии, что экраны установлены на абсолютно одинаковых расстояниях от источника, но на практике это расстояние разное. Следовательно после колапса волновой функции на одном из экранов(который ближе к источнику) на втором экране ничего не регистрировалось бы. Но регистрация есть, а значит и второй фотон.
Вовсе нет, расстояния от детекторов до источника могут быть какими угодно. Сначала передний фронт волны фотона достигает одного детектора, а потом, через некоторое время — второго. А что такое фронт волны? Это — поверхность равной фазы и одинаковой поляризации. Конечно, это несколько упрощенное описание явления (передний фронт сложней устроен). Но суть именно в этом, а не в сказках о запутанных парах фотонов, придуманных Аспэ на основе этих экспериментов ))
Спасибо за разъяснения.
Прошу Вас подтвердить правильно ли я понимаю, что если в указанном эксперименте убрать/исключить разделитель частиц и провести эксперимент с одним фотоном, то мы получим аналогичные по своей сути результаты как если проводили его с разделителем? Ведь фронт волны одного фотона буде распространятся в обе стороны, а коллапс волновой функции происходит исключительно в пределах координат экранов, а не волновой функции целиком. И если использовать не два направления а скажем три, то на каждом детекторе мы получим свои индивидуальные измерения и если не знаем об источнике и количестве фотонов, можем сделать ошибочный вывод , что их(фотонов) было три, а не один.
Вам спасибо за интерес к теме. Мне сейчас некогда, поздней отвечу. Коментарии премодерируются (есть причины), поэтому не сразу отображаются. Повторять нет необходимости ))
Попробую ответить. В опытах Аспэ и других с т.н. «запутанными фотонами» нет разделителей частиц, насколько я понимаю. Коллапс волновой функции — это вульгарно-популяризованное понятие, поэтому не стоит относиться к нему слишком серьезно. Лучше (и точнее) говорить о переходе квантовой системы в стационарное состояние измеряемой величины. Применительно к фотону, который в принципе не имеет «точечной» локализации, понятие измерения нуждается в более широком толковании. В опытах Аспэ измерениями поляризации следует считать акты ее измерения двумя поляризаторами, а не каждым из них по отдельности. Причем эти два акта одного измерения (для одного фотона!) не обязаны происходить одновременно. Это очень естественно, если учесть, что фотон — не частица в общепринятом понимании. Хотя и ведет себя, как частица, в процессе испускания, поглощения и рассеивания атомами. Но распространяется в пространстве, как волна (точнее — волновой пакет). И если Вы станете вот так — шире смотреть на понятие измерения, то противоречие, которое Вы имеете ввиду, не возникает. По-моему гораздо лучше «поступиться принципами», расширив толкование базовых понятий, чем верить в сказки о запутанности в духе псевдо-парадокса ЭПР ))
не специалист, но интересно разобраться в интерпретации. если на далеко разнесенных детекторах регистрируется один и тот же фотон, то откуда следует что он вообще движется, а не является стоячей волной?
А с чего ему быть стоячей волной при отсутствии резонатора? Кроме того реальный фотон — это волновой пакет, а он стоячим быть не может.
я заранее не знаю что за события регистрируют детекторы (отдельные фотоны или один и тот же фотон или суперпозицию разных фотонов), даже не знаю возникли они в ходе интересующего нас эксперимента или независимо от него (кажется в природе нет замкнутых систем). какое свойство можно измерить, чтобы оно показало что детекторами регистрируется один и тот же фотон или два разных если энергии и поляризации таких состояний одинаковы? и как учесть в этом вероятностную природу детектирования, т.е. детектор не всегда будет срабатывать при попадании в него фотона? подойдет ответ указанием на статью(и), доступную в понимании не математику, если такие есть. спс
О самих опытах Аспэ можно почитать здесь http://www.chronos.msu.ru/old/RREPORTS/aspek_teorema_bella.pdf.
спасибо, посмотрел. как я понял, там используется регистрация фотонов на частотах лямда1 и лямда2, которые выделяются соответствующими интерференционными фильтрами. это сразу исключает регистрацию одного и того же фотона разными детекторами. а без фильтров видимо пришлось бы учитывать указываемую вами возможность регистрации одного фотона обоими детекторами.