Пуск Минитмена-3
Проблема уклонения от противоракет становится все более актуальной по мере того, как российские ядерные силы тают http://extremal-mechanics.org/archives/13999, а США настойчиво работают над ПРО http://extremal-mechanics.org/archives/3547. В этой статье дан анализ возможности использовать т.н. настильную траекторию, о которой, применительно к ракетам «Тополь-М» и «Ярс», сложилась шапкозакидательская мифология http://extremal-mechanics.org/archives/142. Мы снова будем моделировать полет боевой части МБР (разделяющейся боеголовки или моноблока), которая в дальнейшем называется БЧ.
Активный участок траектории МБР (см. фото), когда последовательно работают моторы трех ступеней, длится 2.5 — 5 минут и обычно заканчивается на высоте 200 — 400 км над Землей. После этого начинается свободный полет БЧ по баллистической кривой, который завершается попаданием в цель. Скорость БЧ в момент освобождения достигает 7 — 7.5 км/сек. В случае ракеты с разделяющимися боеголовками т.н. bus или платформа разведения в течении нескольких минут рассеивает смертоносный груз, выводя каждую БЧ на траекторию полета к своей цели. Апогей , т.е. максимальная высота траектории над Землей варьируется в диапазоне 750 — 1 200 км.
Мы смоделируем полет БЧ по баллистической кривой, который начинается на высоте км при скорости
и завершается в точке, которая находится на расстоянии
км по поверхности Земного шара (от места пересечения с ней отрезка, соединяющего начало кривой с центром Земли). Еще одним параметром, определяющим баллистическую траекторию, является начальный угол тангажа
— угол между вектором
и горизонталью. Заметим, что дальность в 10 000 км достаточна, чтобы поразить любую точку США ракетой, запущенной из глубины территории России. При этом между Москвой и Нью-Йорком всего 7 500 км.
Типичное время полета БЧ на межконтинентальную дальность равно 25 — 30 мин. Плюс к этому время разгона на активном участке и минус время выяснения того, куда направились ракеты вероятного противника — получим около пол-часа на то, чтобы спасти правительство, активировать центры военного управления и нанести встречный удар. Однако полетное время БРПЛ может оказаться существенно меньшим в зависимости от того, как близко субмарина смогла подобраться к моменту начала войны.
Компьютерная анимация полета Минитмена-3. На видео активный участок кажется длинным, хотя он измеряется сотнями км. Видно, что БЧ поворачивается перед входом в атмосферу, чтобы войти под правильным углом и не сбиться с курса под действием аэродинамического сопротивления.
Чем быстрей БЧ достигнет своей цели, тем выше вероятность успеха при контрсиловом ударе http://extremal-mechanics.org/archives/2574. Уменьшить время полета по баллистической кривой можно за счет уменьшения начального тангажа
и увеличения начальной скорости
. Получится более пологая и короткая траектория (при той же дальности полета), которая считается предпочтительной для преодоления ПРО. Например «Тополю» приписывают настильную траекторию, которая якобы делает БЧ неуязвимой. C чем связана ее «неузявимость»?
Например разница в скоростях двух БЧ, которые находятся в апогеях 500 и 1100 км — 6.9 и 5.9 км/сек соответственно, вряд ли существенна для наведения ракеты-перехватчика. Более того, достать низко летящую БЧ намного проще. Может быть дело в том, что чем ниже траектория, тем короче дистанция прямой видимости для радаров ПРО? Последняя равна , где
км — радиус Земли. На высоте
км получим
км, а при
км
км. Если понизить апогей до
км, то на всей траектории будем иметь
км — это не так уж мало! Учитывая, что в обнаружении целей для ПРО и наведении перехватчиков участвуют спутники и радары на кораблях, приближение горизонта видимости за счет снижения высоты полета не выглядит критическим фактором. Хотя возможно, что относительно низко летящая БЧ все-таки затрудняет ПРО. Мы не рассматриваем здесь этот вопрос, т.к. сама возможность прижаться к матери Земле выглядит крайне сомнительно.
Начнем с классической МБР типа Минитмен-3, апогей которой оценивают в 1100 км. Тогда время баллистического полета на дальность км при
км/сек и
град. составит 30 минут (
сек). Уравнения движения БЧ в поле гравитации Земли выписаны в статье http://extremal-mechanics.org/archives/142, а здесь решается в MathCad система дифф. уравнений, которая получена после понижения порядка.
Читатель может без труда провести свои расчеты, скопировав этот рабочий лист. Нужно лишь задать дистанцию до цели (км) вдоль поверхности Земли и время
(сек) полета БЧ по баллистической траектории. Угол
(град) и скорость
(км/сек), которые дают такую траекторию, будут найдены автоматически и их значения видны внизу листа («уточненный угол тангажа» и «уточненная скорость»). Заметим, что это — точная модель процесса, но без учета аэродинамического сопротивления. Последнее существенно изменит параметры полета только при входе плотные слои атмосферы, что произойдет ниже отметки высоты в 100 км. При этом БЧ претерпевает такой нагрев, что температура отдельных участков ее поверхности может достигать 7 000 K. Это и есть проблема настильных траекторий, которую мы рассмотрим ниже.
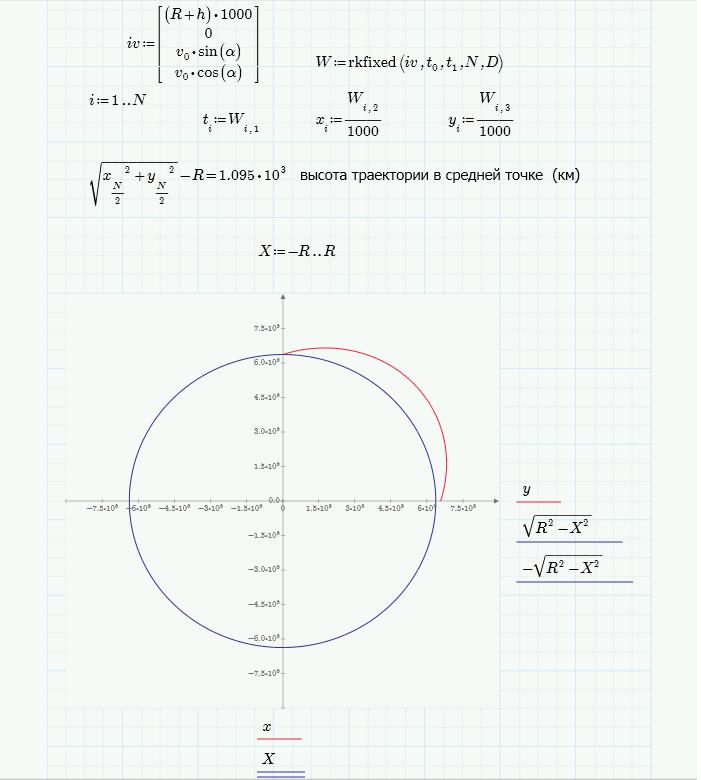
На следующем рисунке дана недостающая часть расчетов и траектория Минитмен-3. Синяя окружность — Земля в масштабе траектории. Апогей равен 1095 км. Начальная точка траектории (), расположенная на высоте
км, отчетливо видна на оси Х.
Полет на 10 000 км снятой с вооружения MX «Peacekeeper» предположительно продлился бы 28 минут при км/сек,
град и с апогеем 860 км. По видимому, существенно более пологие траектории нецелесообразны из-за чрезмерного нагрева при снижении на цель. Однако попробуем смоделировать баллистический полет на 10 000 км с апогеем 500 км, который пока еще нельзя назвать настильным. Он начинается при
км/сек и
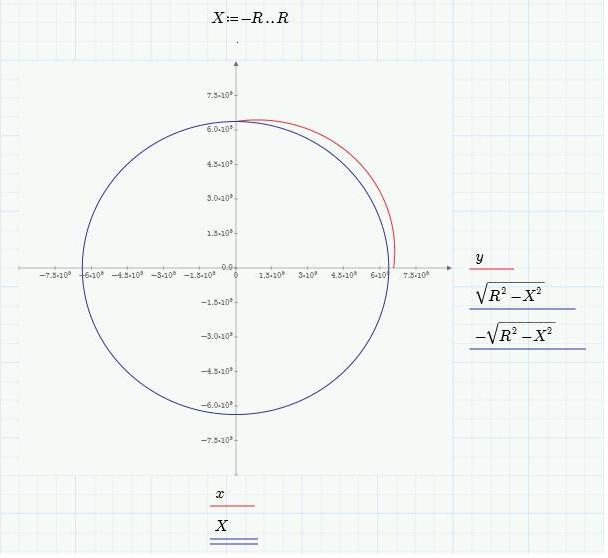
град, а время полета составит 25 минут (без активного участка, у MX он длился 3.3 мин). Более точно апогей = 506 км. Эта пологая траектория выглядит так:
Для оценки аэродинамического нагрева в верхних слоях атмосферы годится формула , где
— тепловой поток Вт/кв.м,
— скорость,
— плотность воздуха,
— угол между вектором скорости потока и нормалью к поверхности, которую он обтекает. Для БЧ в форме конуса с углом при вершине 30 град
град и
(1)
Определить плотность атмосферы поможет калькулятор http://www.digitaldutch.com/atmoscalc/. Так на высоте 35 км плотность , на 30 км
, а на 20 км
кг/куб.м. Для оценки величины
между отметками 35 и 20 км можно принять в качестве средней
кг/куб.м. Диапазон высот выбран из соображений применимости формулы (1) (только в разреженной атмосфере). Это — малая часть «воздушной подушки», в которую на скорости выше 7 км/сек врежется БЧ. Однако слоя в 20 - 35 км достаточно, чтобы оценить аэродинамические эффекты.
Из (1) при м/сек получим тепловой поток в 1 ГВт (!) на кв.м поверхности БЧ. Время снижения с высоты 35 до 20 км составит 13.2 сек, за это время каждый кв.см поверхности получит 1.3 МДж тепла. Этого хватит, чтобы расплавить и испарить вольфрамовую обшивку с толщиной 13 см! При диаметре основания конуса в 1 м такая оболочка весила бы 7.5 тонн, однако вся БЧ «Тополя-М» весит чуть больше тонны. Но самое интересное начнется в тропосфере (ниже 10 км), где плотность воздуха достигнет 0.4 и почти линейно возрастет до 1.2 кг/куб.м у поверхности Земли. Этот этап полета будет длиться 8.6 сек и очевидно, что поток тепла увеличится на порядок. Можно с уверенностью утверждать, что никакая разумная теплозащита, будь то графитовая или керамическая, и в том числе абляционное покрытие не спасет БЧ от чудовищного перегрева.
Для траектории Минитмен-3 ситуация с нагревом выглядит менее драматичной. А именно, ниже 10 км БЧ будет находиться 4.3 сек, а время снижения от 35 до 20 км сократилось до 6.6 сек. И все равно при м/сек и
получим из (1) оценку потока тепла в 890 МВт на кв.м поверхности БЧ только на этом участке траектории! Но аэродинамический нагрев начнется выше 50 км и даже там будет настолько серьезным, что за время снижения с 50 до 35 км (6.6 сек) количество тепла на кв.см поверхности превысит 30 КДж. Это — оценка стойкости термически защищенных БЧ от поражения лазерным оружием, которая применялась в СССР при анализе «Звездных войн» (СОИ).
Пучок разделившихся боеголовок проходит через облака.
Но что позволяет БЧ Минитмена-3 и других «классических» МБР достигать хотя бы границы тропосферы, не сгорая полностью в стратосфере, как метеор? Ответ: аэродинамическое торможение, которое начнется ниже отметки в 100 км. Для этого некоторые БЧ перед входом в атмосферу разворачиваются основанием конуса в направлении полета, а другие имеют затупленные носовые наконечники. В обоих случаях перед БЧ формируется скачок давления, который служит своего рода щитом и препятствует обтеканию потоком, что значительно уменьшает нагрев.
Но в результате БЧ сбрасывает скорость до примерно 3 км/сек при входе в тропосферу. Из формулы (1) при м/сек и
кг/куб.м получим тепловой поток в 70 МВт на кв.м поверхности БЧ. При такой скорости время снижения с 35 до 20 км составило бы 15.3 сек, так что каждый кв.см поверхности получил бы не меньше 100 КДж тепла. Это очень сильный нагрев, но от него БЧ спасают теплозащитные покрытия из графита, тефлона, углепластика и т.д.. Таким образом, единственным способом избежать судьбы метеора является аэродинамическое торможение БЧ до в 2.5 — 3 раза меньшей скорости (после чего она все равно горит в полете, но успевает сработать).
Итак БЧ, имеющая достаточно отвесную траекторию, при входе в плотные слои атмосферы работает в экстремальном режиме с точки зрения аэродинамического нагрева. Самые грозные МБР типа МХ или SS-18 выводят свои боеголовки на траектории с несколько меньшим апогеем (~ 850 км), Однако, как мы видели, пологая траектория с апогеем 500 км почти в два раза увеличивает время пребывания БЧ в плотных слоях атмосферы, чем значительно осложняет задачу ее тепловой защиты. При этом выигрыш во времени достижения цели на удалении 10 000 км для такой БЧ составит всего лишь 3 минуты, что вряд ли оправдает дополнительные сложности с теплозащитой. При этом следует заметить, что из-за существенно большего времени полета в плотных слоях атмосферы такая БЧ быстрей лишится «свиты» из ложных целей и источников помех, которые отстанут от нее за счет намного меньшей массы. Это облегчит задачу селекции цели для ПРО.
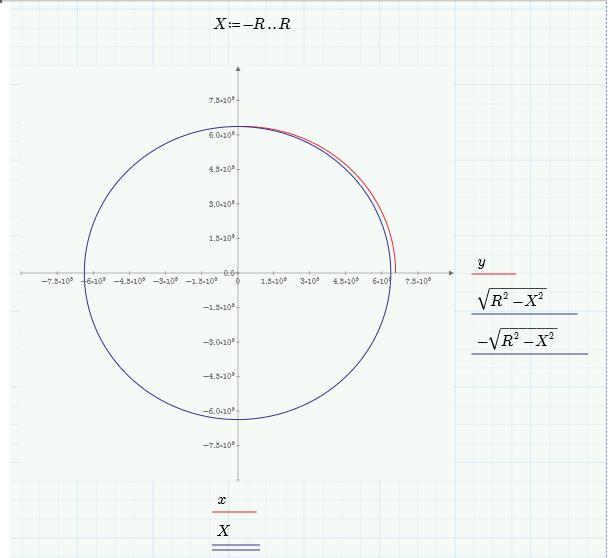
Что касается настильной траектории «Тополя-М», которая проходит чуть ли не параллельно земной поверхности на высоте 200 — 250 км, то это бред, придуманный журналистами. Предельный случай такой траектории получается в MathCad-е при начальных скорости км/сек и угле тангажа
град, и выглядит это вот как:
Такой полет на дальность 10 000 км продлится 22 минуты, если аэродинамика не внесет свои коррективы. А она внесет их обязательно! По этой траектории БЧ будет лететь ниже 50 км дольше 3-х минут. Даже если принять плотность (как на высоте 50 км), то из формулы (1) за 3 мин получится 1 МДж тепла на кв.см поверхности. На самом деле эта оценка будет на 1 — 2 порядка больше, т.к. плотность воздуха возрастает.
Вместе с тем ясно, что работа сил трения пойдет на уменьшение кинетической энергии БЧ, большая часть которой трансформируется в тепло. Поэтому можно грубо оценить снижение скорости БЧ за эти 3 минуты, как , где
— количество тепла. Cчитая площадь боковой поверхности конуса 3 кв.м, получим
км/сек! Этот результат не точен, но он ясно показывает, что если БЧ не сгорит от аэродинамического трения, то резко снизит скорость и не долетит до цели тысячи километров. Настильная траектория «Тополя-М» — это пропагандистский миф.
Дмитрий Зотьев





В этой статье есть некоторые оценки возможности БЧ маневрировать в полете http://extremal-mechanics.org/archives/3547
Относительно новая статья на близкую тему http://extremal-mechanics.org/archives/15162
Формула (1) для оценки теплового потока не подходит.
Во-первых, по этой формуле значения получаются завышенными как минимум на порядок даже для изотермической поверхности. Во-вторых, тепловой поток сильно зависит от разницы температур торможения и температуры поверхности. В формуле это никак не отражено. В начальный момент времени он может быть достаточно большим, но по мере нагрева поверхности тела тепловой поток падает еще на порядок/порядки. Может в нуль обратиться, а при снижении скорости (если температура поверхности временно станет выше торможения) даже стать отрицательным, т. е. вместо нагрева будет остывание. Кроме того тепловой поток распределен неравномерно: на хвостике он значительно ниже чем на носике (в нулевой момент времени). Поэтому не нужно всю ракету обшивать тоннами вольфрама, графита и т.д.
1. Я формулу (1) не сам придумал вообще-то, а взял из физической энциклопедии, посмотрите в конце статьи http://femto.com.ua/articles/part_1/0243.html. Формула выражает тепловой поток через скорость аппарата и плотность воздуха при условии ламинарного обтекания разряженным воздухом (в стратосфере).
2. Тепловой поток всегда пропорционален градиенту температур. Вопрос в том, о каком потоке идет речь? От боеголовки в атмосферу? Если так, то при чем здесь эта формула? Она же описывает аэродинамический нагрев, а не остывание за счет других эффектов (см. ниже). И что такое температура торможения? Формула (1) дает, фактически, мощность сил аэродинамического сопротивления на кв. метр поверхности, а она НЕ зависит от ее температуры.
3. По поводу остывания при нагреве — сильно преувеличено и, вообше говоря, неверно. Это может быть эффективным только за счет конвекции, но при ламинарном обтекании она незначительна. Дело в том, что касательный к поверхности поток воздуха не столько отводит от нее тепло, сколько нагревает за счет трения. При малой турбулентности конвекция мала. Если боеголовка разворачивается тупым концом конуса или имеет затупленный наконечник (это зависит от конструкции), то нагрев резко снижается за счет появления ударной волны (и турбулентности конечно). На этом же принципе работает теплозащитный экран спускаемых аппаратов космических кораблей («Союз», «Джемини», «Аполлон», статья об этом http://extremal-mechanics.org/archives/20712). Теплопроводность воздуха ничтожна. Инфракрасное же излучение относительно мало, просто посчитайте с помощью закона Стефана-Больцмана.
4. При ламинарном обтекании греется вся поверхность конуса, носик возможно больше, хотя скорее всего меньше из-за ударной волны перед ним. Что это меняет по существу?
Итог: при ламинарном обтекании эффекты остывания незначительны по сравнению с аэродинамическоим нагревом. Мои оценки сделаны именно для случая ламинарного обтекания в обоснование того, что боеголовка вынуждена сбрасывать скорость при входе в атмосферу и не способна летать по т.н. настильной траектории. Разумеется, в режиме торможения с ударной волной сжатия данная формула неприменима. Этот факт никак не опровергает мою статью.
Вместо того, чтобы придумывать скоропалительные возражения, приведите пожалуйста формулу теплового потока, которая по вашему является правильной. Сайт http://femto.com.ua/articles/part_1/0243.html публикует статьи из Физического Энциклопедического Словаря или аналогичного справочника по физике. Чтобы с ним спорить, нужно иметь более веские основания, чем желание выступить в защиту мифа о настильных траекториях МБР Тополиного семейства.
1.По указанной ссылке оговаривается, что формула используется для » тел, движущихся в верх. слоях атмосферы, где режим обтекания является свободномолекулярным, т. е. длина свободного пробега молекул газа соизмерима или даже превышает размеры тела». Т.е. когда нет пограничного слоя. Верхние слои атмосферы — это где-то выше 50 км.
У вас формула (1) применяется для высот 20-35 км и для скоростей выше 7000 м/с (Число Маха около 25). Для 35 км: ro= 0.008, mu = 1,5*10^-5, V=7000 => Re=3 733 333 * L > 1000. Это пограничный слой!
Для оценки тепловых потоков в таких случаях (в т.ч. 20-35 км) используется формула Фей-Риддела или более простые аналоги. http://engjournal.ru/articles/1243/1243.pdf (5)-(8)
2. Когда тело обтекается сверх- и гиперзвуковым потоком газа, то около тела газ тормозится и кинетическая энергия переходит в тепловую. Около тела образуется слой очень горячего газа, который начинает нагревать тело. Чем быстрее движется газ, а значит сильнее затормозился, тем больше температура. Максимально возможная температура — это температура торможения газа, когда вся кинетическая энергия перешла в тепловую. Трение — это просто процесс, который способствует переводу кинетической энергии в тепловую. Если кто-нибудь придумает способ нагреть тело значительно сильнее, чем нагретый газ вокруг него, то тело (благодаря отличной скоростной вентиляции) просто передаст тепло этому газу.
3. Просто представьте, что ракета неслась со скоростью 7000 м/с, нагрелась местами до 3000-4000 К, а потом быстро уменьшила свою скорость, допустим до 0 или 100 м/с или до 1000 м/с и т.д. Из-за чего она будет нагреваться? Она начнет остывать, потому что вокруг нее газ менее нагретый, чем сама ракета.
4. В начальный момент времени, когда температура по всему телу одинакова, и при ламинарном сверхзвуковом движении тела, максимум теплового потока находится в носике ракеты. Это дают все формулы, которые естественно получены с учетом ударных волн. В дальнейшем все зависит от температуры поверхности и есть или нет разрушения, разложения материала и т.д. В силу этого, к разным частям ракеты подход должен быть разным.
Вы пытаетесь оспорить мою статью, однако не даете своих числовых оценок. Такого рода критика допустима лишь в том случае, когда ошибки грубы и очевидны. Вы ни одной такой не обнаружили. Просто цепляетесь ко всему, в чем видите повод прицепиться. Безотносительно к тому, насколько ваши возражения существенны. Это — не критика, а критиканство.
1. В статье есть оговорка о том, что формула (1) применяется в разряженной атмосфере. На какой именно высоте — не уточнял. Понятно, что на высотах 20 — 35 ее применимость под вопросом, но и на 50 км вопрос остается. На 30 и 50 км длина свободного пробега составляет доли миллиметра, а на 80 км «аж целых» 1 — 2 см. Во всех этих случаях говорить о сравнимости с размерами боеголовки не приходится.
Условие свободномолекулярности обтекания нужно для того, чтобы исключить образование ударных волн. В статье рассматривался случай, когда боеголовка входит в атмосферу острием конуса, следуя пологой или мифологической, настильной траектории. Тогда на высотах 20 и 50 км обтекание можно считать ламинарным в том смысле, что НЕ формируются ударные волны, которые поглощали бы значительную долю кинетической энергии. Именно такой режим обтекания я назвал ламинарным (уж простите великодушно не специалиста в аэродинамике!).
По поводу ламинарного или турбулентного пограничного слоя — в такие тонкости я не вдавался. Но в контексте образования ударных волн роль тонкого, пограничного слоя явно незначительна http://mash-xxl.info/page/164228253133233226061051139239184149193042050153/,
На мой взгляд, то же касается конвективного теплоотвода.
Но если принять во внимание турбулентный пограничный слой, то, как известно, аэродинамический нагрев будет на 2 порядка больше по сравнению с ламинарным слоем. Таким образом, описанная в статье картина не станет менее драматичной с точки зрения теплового режима боеголовки.
Ваша оценка для числа Рейнольдса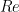 полностью бессодержательна, т.к. неравенство
полностью бессодержательна, т.к. неравенство  выполнялось бы даже при скорости
выполнялось бы даже при скорости  м/сек! (
м/сек! (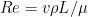 ). Кроме того, число 1 000 не будет критическим значением. При обтекании тел воздушным потоком критические
). Кроме того, число 1 000 не будет критическим значением. При обтекании тел воздушным потоком критические 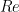 выражаются в сотнях тысяч.
выражаются в сотнях тысяч.
Наивно думать, что формула, применимая на высоте 50 км, категорически не может быть применена при возрастании плотности воздуха в 8 раз (35 км). Тем более, что речь идет о грубых оценках, а не точных расчетах. .
Что касается формулы Фей-Риддела и статьи, которую Вы указали, то я заглянул туда, не поленился. Статья и эта формула посвящены теплообмену в критических точках сферы. В моей статье речь где-то шла о сфере? В исходной статье Фей-Риделла 1959 года рассматривалось обтекание затупленного носового наконечника. Точно такой имели тогдашние МБР «Атлас». Таким образом, в рассмотренной мною задаче данная формула едва ли применима вместе с ее «более простыми аналогами».
Вам стоило сделать альтернативный расчет по формуле Фей-Риделла вместо того, чтобы с умным видом тыкать пальцем в статью, которую вы, похоже, внимательно не просмотрели.
2. Согласен, вначале нагревается слой воздуха, который затем нагревает обшивку. Движение молекул воздуха хаотизируется от почти упругих столкновений с поверхностью (в системе отсчета боеголовки), что означает преобразование кинетической энергии в тепло. Но что это меняет по существу? Ведь поток тепла пропорционален градиенту температуры. Это означает, что за счет нагревания обшивки до максимальной температуры средний поток тепла уменьшится в 2 раза (грубо). Поскольку мои оценки относятся в основном к порядкам величин, по сути ничего не изменится.
3. Я не рассматривал ситуацию, когда боеголовка затормозила до 1 000 м/сек.
4. Из сказанного вами следует, что поток тепла через носик нужно считать отдельно. Считайте, если вам угодно. Но его доля в общем потоке через поверхность конической боеголовки будет незначительной.
Естественно, что мои оценки весьма приблизительны, в статье этот факт не скрывается. Вам лень сделать хоть какие-то оценки, при этом вы требуете от меня написать диссертацию о тепловом режиме полета боеголовки МБР )) Если вы — технически грамотный человек, что выглядит правдоподобно, то должны бы понимать такие вещи.
В следующий раз прошу вас дать свои оценки теплового потока, если желаете и дальше возражать. Я не хочу тратить на ответы больше времени, чем вы на свои придирки. И вообще — смотрите пожалуйста в корень статьи! Вам хочется верить в ура-патриотические глупости о том, что БЧ «тополя», «ярса» и прочих летают по настильной траектории, еще и маневрируя при этом? Тогда потрудитесь сделать обоснованные, числовые оценки. Или не отнимайте мое время, если вам жалко своего ))
афтор, таки значит БЧ минитмена действуют иные законы физики ?
ведь время пролета через атмосферу у него незначительно отличается,
ну а если БЧ минитмена может тормозить — то и БЧ тополя может тормозить, не так ли ?
иначе все БЧ тополя успарялись бы нахрен, если верить утверждениям афтора.
советую так же обратить внимание на предположения что траектория
могет быть комбинированной, пологой на активном участке и отвесной и какой угодно на .
среднем и конечном.
А я вам советую подтянуть русский язык, внимательней читать статьи, которые пытаетесь критиковать, и больше не писать глупостей.
Интересная статья, в которой рассматриваются настильные траектории БРПЛ при малых дальностях полета (1 875 и 3 000 км) http://extremal-mechanics.org/wp-content/uploads/2018/03/sgsr03gronlund.pdf. Оценки теплового нагрева на высотах 20 — 30 км существенно отличаются от тех, которые представлены в статье «Жар стратосферы». Значения потока тепла через поверхность боеголовки, получаемые из формул на стр. 55, меньше на 2 — 3 порядка.
При этом уравнение (3.1) на стр. 53 равносильно формуле (1) из моей статьи, если разделить ее на 2. Делить на 2 действительно нужно, т.к. тепло, выделяемое при аэродинамическом нагреве согласно (1), делится пополам между боеголовкой и окружающим воздухом. Я же «отдал» все тепло боеголовке. Эта ошибка не влияет на выводы статьи «Жар стратосферы», которая основана на оценках тепловых потоков с точностью до порядка величины. Но авторы статьи о настильных траекториях БРПЛ утверждают, что формула (3.1) применима выше 130 км, с чем трудно согласиться. Они исходят из формальной оценки длины свободного пробега молекул воздуха, но очевидно, что формула (3.1) применима и на значительно меньших высотах. Характер взаимодействия набегающего потока с поверхностью существенно изменится в том случае, когда ее ламинарное обтекание сменится формированием скачка уплотнения воздуха перед носом боеголовки с образованием ударных волн. Высота, на которой эти аэродинамические эффекты сделают неприменимой формулу (1), зависит от скорости и геометрии боеголовки. В случае заостренного конуса, который рассматривается в моей статье, высота «неприменимости» (1), по-видимому, кратно меньше 130 км.
Авторы статьи рассматривают боеголовки с затупленным (скругленным радиуса около 5 см) носовым наконечником, которые применялись в МБР первого поколения («Атлас», «Титан»). Это видно из текста, а также из того, что формулы на стр. 55 взяты из книги 1961 года. Такие боеголовки именно для того и затупляли, чтобы уменьшить нагрев за счет торможения с переходом большей части кинетической энергии не в тепло, а в энергию ударных волн в воздухе. Для такой боеголовки при скорости 7 285 км/сек (значение, для которого в моей статье получен 1 ГВт на кв.м) формула (3.5) дает поток тепла через носовой наконечник около 50 МВт на кв.м. В этом случае поток тепла через боковую поверхность, которое переносится конвекцией от носовой части, еще на порядок ниже.
Это наглядно показывает эффективность такой термической защиты, но очевидно, что боеголовка с затупленным носовым наконечником не сможет двигаться по настильной траектории (существенно ниже 150 км), сохраняя заданный профиль скорости. Для стрельбы на дальность меньше 2 000 км, о которой в основном идет речь в обсуждаемой статье, эти потери скорости могут оказаться непринципиальными (легко посчитать, но лень). Но боеголовка МБР не сможет лететь по настильной траектории на межконтинентальную дальность, что обосновывается в статье «Жар стратосферы».
Авторы статьи о настильных траекториях БРПЛ отмечают важный факт: при полете боеголовки на относительно малой высоте (50 — 100 км) резко возрастает ее разброс вокруг цели, т.е, падает точность. Промах может достигать нескольких км по дальности (таблица на стр. 31).
С чем может быть связана некоторая девиация следов от боевых блоков в атмосфере, как на фото в статье? Есть ещё более выразительный снимок — https://sun9-56.userapi.com/c854416/v854416752/d22e1/L1UMm4Tqzx4.jpg
Первое, что приходит на ум — это длинная выдержка и камера на движущейся платформе (самолёте), поскольку на фото с неподвижных камер треки преимущественно идеально прямые. Но в свою очередь здесь фото однозначно с самолёта https://i.pinimg.com/564x/6c/8b/83/6c8b83fa2bf512498520de46d3a086d5.jpg , а треки ровные, как под линеечку…
Девиация может быть связана с кувырканием боеголовок, потерявших ориентацию. Или с неоднородным сгоранием наконечника конуса. Последнее явление — серьезная проблема, вносящая погрешность попадания в сотни метров. С ней как-то справились еще в 70-х. На фото может быть эксперимент на эту тему. Если фото современное, то боеголовки могут быть китайскими. Наконец, может быть эксперимент с аэродинамическим маневрированием. Такие проводились когда-то. Нет никаких проблем заставить боеголовку вот так рыскать при входе в атмосферу, только отклонение от цели будет намного больше. При стрельбе по городам это не очень принципиально. В любом случае данные снимки никак не подтверждают мифы путинской пропаганды о маневрирующих на протяжении всего полета боевых блоках.
Фото американское 100%, но не суть.
Неравномерная абляция — да, это первое, о чём я подумал. Но ведь вроде как ББ закручиваются ещё на заатмосферном участке, а значит она должна быть равномерной. Кроме того, на некоторых «стационарных» снимках чётко видно, как ББ описывает плавный штопор (привести не могу, заново не нашёл). Но на остальных этого нет.
Хочу обозначить, что я ни в коем случае не пытался привести это, как контраргумент на Ваши доводы. Совершенно очевидно, что некие манёвры ББ с целью преодоления ПРО — это бред по самой сути. Но эффект на фото интересен сам по себе.
Если наконечник горит неравномерно, то вращением этот эффект полностью компенсировать нельзя. Он же горит неравномерно не потому, что нет вращения, а из-за внутренней неоднородности материала. «Штопор» здесь и должен получаться, как мне кажется. Если снимки штатовские и более-менее современные, то, видимо, эксперимент с аэродинамическим маневрированием. Хотя зачем им это?
Дата снимка неизвестна, но ранее середины 80-х подобных фото вроде как нет. К этому времени проблемы с неоднородностью уж точно должны бы быть решены. Я всё же склоняюсь к чисто «фотографическому» эффекту. С этим могут быть связаны самые разнообразные причуды, о которых невозможно судить без специальных знаний в данной сфере.
Я тоже вначале так подумал. Если камеры дергается в руках, то, казалось бы, такой эффект возможен. Но смущает скорость боеголовок, они проносятся через эту область за доли секунды. Как быстро должна колебаться камера? К тому же они рыскают по разному, а должны были бы одинаково, если дело в колебаниях камеры. Так что если это «фотоэффект» (да простит меня Эйнштейн), то какой-то хитрый ))
Я потому и взял «фотографический» в кавычки, поскольку даже представить не могу какие эффекты могут проявиться в данной области. Тем не менее, согласитесь, фото озадачивает:)
1-й снимок — полет на большой высоте в разряженной атмосфере с неравномерным изменением плотности воздуха по высоте и ее локальной неоднородностью по эшелону, соответственно — разный угол преломления на различных высотах и локациях. Т.е. здесь непрямолинейночть траекторий — лишь оптический эффект.
2-ой снимок — заключительный участок траектории, полет в плотной атмосфере, где относительные значения неоднородности плотности значительно ниже и не влияют заметно на угол преломления.
Да никто и никогда не собирался использовать настильную траекторию на максимальную дальность. Она предназначена для минимальных дальностей, когда выигрыш во времени уже существенен. Соответственно, время полета в атмосфере невелико.
А зачем тогда путинская пропаганда врет о таких настильных траекториях уже лет 10? Ведь речь в статье шла об этом вранье. На максимальную дальность — это на какую? Какая дальность, по Вашему, позволяет использовать т.н. настильную траекторию? И что считать настильной траекторией в этом контексте? Насколько я могу судить, траектории с апогеем 100 — 200 км могут использоваться разве лишь при запуске с подводной лодки, на расстоянии 1 000 — 2 000 км от цели (грубая оценка).
Не путинская пропаганда, а безграмотные журналюги. Когда читаешь что они пишут, волосы дыбом встают на всем теле.
Максимальная дальность имеется в виду для данной ракеты.
Журнашлюхи распространяют путинскую пропаганду.
Угол между вектором скорости и горизонталью называется углом бросания. Угол тангажа — это угол между продольной осью ЛА и плоскостью стартового горизонта.
Мне кажется, что Вы перепутали эти два угла между собой. Судя по названию, угол бросания как раз и должен отмеряться от стартового горизонта.
Угол бросания определяется относительно местного горизонта.
Но определяется он в момент «бросания», например при выстреле из орудия. А при полете ракеты угол между ее продольной осью и местным горизонтом все же называется углом тангажа.
Угол тангажа определяется относительно стартового горизонта, положение которого фиксируется гироскопическими приборами в момент старта и сохраняется во время полета.
Но это же нелепо! Если ракета пролетит над Землей в космосе, допустим, 10 000 км, то таким образом определенный «угол тангажа» изменится грубо на 90 градусов. В чем тогда его смысл? Я по-прежнему считаю, что вы ошибаетесь. И если не найдется более весомых аргументов, то на на этом и закончим препирательства.
Формирование траектории осуществляется изменением направления продольной оси ЛА и, следовательно, вектора тяги двигательной установки. Так как в инерциальной системе управления не используется никакая другая информация (в том числе о положении местного горизонта), кроме той, которая была зафиксирована в момент старта, то программа изменения угловой ориентации ЛА (тангаж, рыскание, крен) задается и регулируется относительно осей начальной стартовой системы координат,.
Если этого недостаточно, откройте любой учебник по баллистике, напр., Ю.Г. Сихарулидзе. Баллистика летательных аппаратов. М. Наука, 1982.
Я не собираюсь открывать учебник по баллистике, т.к. не я на вашем сайте, а вы на моем вылезли с менторскими замечаниями. Вам и доказывать свою правоту! Поэтому извольте указать, где именно в указанном учебнике угол тангажа определяется так, как вы заявляете. На мой взгляд это — чепуха, если речь не идет о выстреле на малую дальность, при котором поверхность Земли можно считать плоской. Если же учитывать кривизну земной поверхности, то для баллистического расчета с учетом коррекций траектории необходимо контролировать угол наклона продольной оси к местному горизонту, а не только использовать угол тангажа при запуске (кстати он меняется, начиная с 90 градусов). Хватит уже изображать из себя специалиста — просто покажите определение угла тангажа, подтверждающее вашу правоту. Хотя, независимо от этого, сей терминологический спор не стоил выеденного яйца.
На стр. 14 указанного учебника читаем: «Стартовая система координат … используется для определения текущего положения ЛА относительно места старта…». На стр. 15: «Для упрощения интегрирования уравнений движения центра масс удобно пользоваться начальной стартовой системой координат, которая совпадает со стартовой в момент запуска, а в дальнейшем не меняет своей ориентации относительно абсолютного пространства (звезд), т.е. является инерциальной». На стр. 17: «В качестве примера рассмотрим расчет матрицы направляющих косинусов между осями начальной стартовой (инерциальной) Онxстzст и связанной Oxyz систем координат. … Угол между продольной осью ЛА и плоскостью Онxстzст называют углом тангажа. Эти углы, чаще всего используемые в баллистике, отличаются от соответствующих углов, определяемых согласно ГОСТ 20058-74 в неинерциальной системе координат, связанных с местной вертикалью».
В книге Р.Ф. Аппазов, О.Г. Сытин. «Методы проектирования траекторий носителей и спутников Земли». М.Наука, 1987 г. на стр. 43 читаем: «При полете ЛА относительная ориентация осей связанной и начально-стартовой систем координат меняется. Будем определять ее тремя углами, которые обычно и фиксируются чувствительными элементами гироскопических приборов и относительно которых ведется процесс управления угловым положением ЛА. Это так называемые углы тангажа , рыскания и крена ». (Для справки: Рефат Фазылович Аппазов был начальником отдела баллистики в конструкторском бюро С.П. Королева).
В работе «Основы моделирования движения ракет: Учебное пособие/Ю. А. Мареев, В. И. Гончаренко, А. И. Четин; Под. ред. А.И. Четина. –М.:Изд-во МАИ-ПРИНТ, 2008.» на стр. 38 : «Угол между продольной осью ракеты и плоскостью стартового горизонта называют углом тангажа».
В книге « Ю.М.Николаев, Ю.С. Соломонов. Инженерное проектирование баллистических ракет с РДТТ. М. 1979 г.» на рис 2.2 (стр. 47) показан угол тангажа, отсчитываемый от плоскости стартового горизонта. (Для справки: Юрий Семенович Соломонов – Генеральный конструктор Московского института теплотехники).
Sapienti sat?
Знаю Соломонова, даже комментировал его рассуждения о несуществующем Сармате и еще кое-о-чем.
А все-таки зря вы надули этот пузырь своей самоуверенностью. Читайте ГОСТ 20058-74, на который дана ссылка в вашем комментарии, вот он: http://docs.cntd.ru/document/gost-20058-80. Определение угла тангажа дано в пункте 26. Именно то, о чем я говорю!
При баллистических расчетах используется угол начального тангажа. И что из этого? В книге того же Соломонова прямо говорится об угле тангажа, отсчитываемом от стартового горизонта. То есть термин «угол тангажа» здесь доопределяется, что не отменяет его общий смысл. И это все отнюдь не означает, что угол тангажа всегда отсчитывается от плоскости стартового горизонта.
Как и следовало ожидать, вы устроили спор на пустом месте. Видимо, по делу возразить нечего, а очень хочется. Извиняться вы явно не собираетесь. Но больше не морочьте мне голову пожалуйста.
Все логично.
На старых ракетах не было «астрокоррекции».
Мощности боеголовок, точность попадания и характер целей — были сильно-много-больше.