Почти полвека отделяют человечество от огромного скачка, которым стал маленький шаг человека с лестницы модуля «Орел» на поверхность Луны 20 июля 1969. Тогда всем казалось, что на очереди Марс и пилотируемый полет к красной планете произойдет задолго до конца столетия. Но XX век давно закончился, а такая задача даже не поставлена в формате: «мы полетим туда не потому, что это легко, а потому, что трудно!». Биологические эксперименты вроде «марсианского дома» слишком далеки от технических проблем межпланетного полета, чтобы воспринимать их, как серьезные шаги на этом пути. Блестящие успехи NASA, отправивших на Марс четыре моторобота (Sojourner — «Попутчик» с июля по сентябрь 1997, Spirit — «Дух» с января 2004 до апреля 2010 , Opportunity — «Возможность» с января 2004 по сей день, Curiosity — «Любопытство» с августа 2012 до настоящего времени), были достигнуты в рамках стратегии автоматического исследования всех планет Солнечной системы вместе со спутниками. Но эти вдохновляющие достижения, среди которых Космическая Одиссея «Вояджеров» и свидание с Плутоном http://extremal-mechanics.org/archives/16588, почти не приблизили полет к Марсу, т.к. никто всерьез не разрабатывает марсианскую ракету. В статье рассматривается небесно-механический аспект этой проблемы и предлагается разумный план. Экспедиция к Юпитеру также обсуждается.
ДОРОГА НА МАРС
Эллиптическая орбита Марса имеет перигелий 200 млн. км и афелий 250 млн. км, поэтому кратчайшее расстояние до Земли колеблется в пределах 50 — 100 млн. км. Разница весьма существенна, так что момент старта нужно подбирать. Ближайшее Великое противостояние наступит 27 июля 2018 http://astrobel.ru/info-po-nabludeniam/protivostoyania-marsa.html. Расстояние до Земли составит приблизительно 58 млн. км. Более реалистичной датой служит 10 октября 2020 - следующее противостояние. Хотя и не Великое, но вполне годится, т.к. до Марса будет около 60 млн. км. Несмотря на грандиозность этого проекта, за 4.5 года можно подготовиться, если использовать лишь актуальные космические технологии. Огромные возможности компьютерного моделирования, которых не было у создателей «Сатурна-5″ и «Аполлона», ускорят разработку двигателей и ракетоносителя. Все, что для этого необходимо — политическая воля.
Часто пишут о том, что экспедиция на Марс займет ~2,5 года, из которых на путь туда и обратно уйдет по ~6 месяцев. Предполагается использовать два соседних противостояния, ради чего экипажу придется ~1,5 года ждать обратного рейса. Но проблема выживания на Марсе в течение столь длительного времени является крайне сложной. Людей нужно защитить от радиации, низкой температуры, метеоритов и обеспечить жизненными ресурсами, включая кислород. В том числе водой, которая хотя и есть на Марсе, но абсолютно непригодна для употребления http://hi-news.ru/space/voda-na-marse-najdetsya-li-chuzhaya-zhizn-v-toksichnyx-ruchejkax.html. В фантастических фильмах часто показывают людей, разгуливающих по красной планете без скафандров, что не имеет никакого отношения к реальности. Марс — это враждебный человеку мир, выжить в котором 1,5 года будет трудно. Достаточно сказать, что дневная доза радиации на его поверхности эквивалентна году на Земле. Тревожное напоминание о том, что там лучше долго не задерживаться!
Единственным разумным решением проблемы выживания на Марсе является доставка жилого модуля со всем необходимым, включая биозащиту от космического излучения. Ясно, что его масса будет существенно больше, чем у жилого отсека корабля вместе с системой жизнеобеспечения. Как мы увидим ниже, в любом случае придется строить два сравнимых марсианских корабля. Однако, риск для здоровья и жизни экипажа возрастает. Ведь если за полтора года пребывания на Марсе произойдет что-то нештатное, то в течение многих месяцев помочь никто не сможет. Даже если в запасе на Земле будет подходящий космический корабль!
Если везти марсианскую базу с собой, то это в разы увеличит вес полезной нагрузки, который является критическим параметром. Даже без «домика» на борту, с экипажем из двух человек в спартанских условиях массу корабля едва ли можно сделать меньше 350 тонн в момент выхода на траекторию полета к Марсу. Чтобы только вытащить такой корабль на околоземную орбиту нужен в 3 раза более мощный ракетоноситель, чем Сатурн-5 http://epizodsspace.airbase.ru/bibl/raketostr3/obl.html. Отсюда видно, что марсолет следует собирать на орбите из доставляемых отдельно модулей и там же заправлять горючим.
Ниже мы увидим, что можно обойтись без длительного пребывания на Марсе. Это позволяет вывести на траекторию свободного полета к нему корабль с массой в пределах 400 т. Несколько больше, чем у заправленного ракетоносителя «Союз» (~300) и значительно меньше, чем у «Протона» (~700). Из них ~250 тонн придется на топливо, включая окислитель, для торможения и маневрирования около Марса, и ~100 т составит нетто-масса корабля (т.е. с пустыми баками). Два Аполлона и только половина МКС - не так уж много для почти года в открытом космосе. Горючее для возвращения домой и высадки на Марс (~250 т), а также спускаемый аппарат следует отправить автоматическим, транспортным судном. Для того, чтобы разогнать корабль с нетто-массой ~100 т на околоземной орбите с 1-й космической скорости до 2-й потребуется ~350 т топлива. С учетом гравитационного торможения, которое существенно до удаления от Земли порядка 1 млн. км и становится слабым уже на орбите Луны, его количество возрастает до ~1 600 тонн. Фактическая скорость ухода с околоземной орбиты будет больше 11,2 км/сек, в зависимости от угла тангажа, но через сутки полета она почти стабилизируется на этом значении.
Стоит заметить, что из-за близости Марса к Солнцу важную роль в обеспечении полета энергией сыграют солнечные батареи. На орбите красной планеты их мощность упадет в 2,5 раза, но все еще будет значительной. В качестве дополнительных и аварийных можно использовать радиоизотопные источники энергии, которые в целях безопасности могут быть вынесены за пределы корабля (~1 км) на тросах. Запас жидкого водорода на пути к Марсу послужит биологической защитой от космического излучения. Для этого кабину экипажа следует окружить водородными баками. На обратном пути обеспечить столь эффективную защиту будет невозможно. Но, по крайней мере, экипаж прибудет к Марсу в хорошем состоянии. Доза радиации, которую он получит на пути к Земле, а также в ходе всей миссии не будет представлять опасности для жизни, но может привести к лучевой болезни легкой или средней тяжести. Среднюю тяжесть можно исключить, используя индивидуальные, биозащитные кабинки-пеналы во время сна и отдыха. При возвращении к Земле экипаж может позволить себе только отдыхать. Что касается центробежной гравитации, то ее нетрудно организовать на обратном пути, но сложно при полете к Марсу из-за биозащиты топливными баками.
Марсианский модуль, хотя разумнее высаживать одного космонавта
В дальнейшем нам потребуется простейшая формула Циолковского, которая выражает приращение скорости космического аппарата. Ее можно использовать для кораблей, разгоняющихся/тормозящих в открытом космосе или на орбите, но нельзя для стартующих с Земли:
(1)
где — cкорость, которую аппарат массой
приобретет, затратив на разгон
кг топлива + рабочего тела (для ЖРД то и другое совпадает),
— удельный импульс двигателя, он же скорость газовой струи относительно аппарата. Для лучших ЖРД на кислороде и водороде можно принять
км/сек. Исходя из этого значения будем вести дальнейшие расчеты.
Устоявшееся мнение о том, что марсианскую экспедицию можно осуществить только за период времени между двумя соседними противостояниями, нетрудно объяснить. Орбитальная скорость Марса равна 24,13 км/сек (max), а у Земли — 29,78 км/сек. Таким образом, наша планета быстрей движется вокруг Солнца. Чтобы хотя бы от нее не отставать, стартовав с Марса и двигаясь по его орбите, нужно лететь в 1,4 раза быстрей (отношение радиусов орбит). Таким образом, относительно Солнца корабль должен иметь скорость 41,7 км/сек. Вычитая отсюда 24,13 км/сек, получим скорость относительно Марса 17,57 км/сек. Если корабль стартует с низкой орбиты (3,6 км/сек), то ему нужно ускориться на ~14 км/сек. Согласно формуле (1) потребуется запас топлива, который в 21,5 раза больше веса пустого корабля. С учетом гравитационного торможения, при нетто-массе 100 т стартовая масса на орбите Марса значительно превысит 2 500 тонн. Только для того, чтобы не отставать от Земли! Эти, на первый взгляд, убедительные оценки показывают, что с Марса догнать Землю практически невозможно. Можно пытаться «оторваться» от нее, летя вдогонку Марсу, чтобы в момент прибытия туда наша планета еще оставалась позади. Но аналогичные рассуждения показывают, что для выхода на околомарсианскую орбиту придется сбросить скорость не меньше, чем на 14 км/сек. А это ничуть не проще! Значит нужно ждать следующего противостояния ?
На самом деле эти оценки чересчур грубы. В них не учтен фактор солнечной гравитации, а он весьма значителен. Легко спланировать полет на Марс во времени, используя закон всемирного тяготения и 2-й закон Ньютона. Потребуется следующая система уравнений:
где - координаты космического аппарата в системе отсчета с центром в Солнце,
— гравитационная постоянная,
— массы Солнца, Земли и Марса соответственно,
— радиусы орбит Земли и Марса ,
— угловые скорости этих планет,
— угол между направлениями от Солнца к Земле и Марсу в момент старта корабля. Предполагается, что углы отсчитываются от положительной полуоси Y по часовой стрелке, и в момент
Земля находится на этой полуоси.
Решить эту систему уравнений в MathCad с достаточной точностью невозможно, т.к. в точках расположения планет возникают сингулярности. В самом деле, по мере приближения корабля к планете знаменатель вида стремится к нулю, где
— радиус-вектор корабля и
— радиус-вектор планеты. Функции MathCad, решающие дифф. уравнения, обычно делят отрезок времени на несколько тысяч или десятков тысяч равноотстоящих узлов (по выбору пользователя). При большем их числе становится заметной погрешность, которая возрастает при каждой итерации. Если временной интервал полета к Марсу разделить на 10 000 точек, то шаг сетки будет иметь порядок получаса. За это время корабль преодолеет расстояние порядка 50 тыс. км, которое имеет важное значение вблизи планеты. Например, при уходе с околоземной орбиты 250 км по параболической траектории аппарат, удалившийся от поверхности Земли на 50 000 км, замедлится с 11,2 км/сек до 4,35 км/cек. Но при расчете траектории полета к Марсу такому расстоянию отвечают два первых узла сетки. Поэтому погрешность вычисления скорости во второй временной точке может иметь порядок скорости, что неприемлемо.
Для преодоления этой проблемы следует отдельно рассчитывать движение корабля вблизи планеты на временном интервале в несколько часов, после чего продолжать полученное решение на время полета до Марса, «не долетая» нескольких часов. Эти последние также следует моделировать отдельно с шагом сетки в несколько секунд. Таким образом, следует решать две задачи с двумя гравитирующими центрами (одной планетой в каждой из них можно пренебречь) и задачу с одним гравитирующим центром (Солнце), склеивая полученные решения в картину полета с околоземной орбиты до околомарсианской. Пусть этой подгонкой параметров занимаются космические специалисты, мы же ограничимся анализом движения корабля под действием Солнца и элементарными оценками действия планет. Погрешности, которые при этом возникают, в контексте практического осуществления миссии «Марс» не имеют заметного значения.
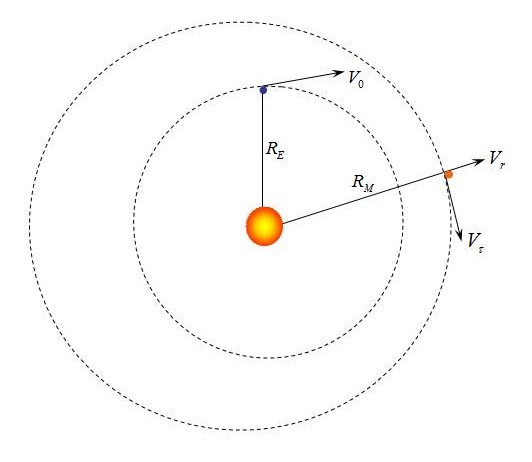
Будем рассматривать задачу движения точки — корабля вокруг гравитирующего центра — Солнца. Тяготения Земли и Марса учтены в значениях их 1-й & 2-й космических скоростей: 7,9 км/сек & 11,2 км/сек и 3,6 км/сек & 5 км/сек соответственно. Они заметно проявляются только на расстояниях в несколько сотен тысяч км от планет. Например, на удалении в 850 тыс. км тяготение Марса составляет около 1% гравитации Солнца, а для Земли аналогичное расстояние 2,6 млн. км. При этом длина траектории полета близка к 250 млн. км (не вычислялась, но можно измерить на графике 1). По мере приближения к Марсу его гравитация способна ускорить корабль на 5 км/сек (2-я космическая скорость), и это будет учтено в наших оценках.
Система дифференциальных уравнений, которая решалась функцией rkfixed() в MathCad, имеет вид
(2)
с начальными условиями ,
млн. км,
,
,
где км/сек — вторая космическая скорость Земли,
км/сек — ее орбитальная скорость,
— начальный угол тангажа. В данном случае его можно определить, как угол между касательной к орбите планеты и вектором начальной скорости корабля относительно планеты. На рисунке скорости относительно Земли и Марса обозначены
и
соответственно,
— орбитальная скорость Марса (24,13 км/сек).
Решая систему (2) для различных значений нетрудно выбрать траекторию полета с начальной скоростью 11,2 км/cек относительно Земли. Последняя минимально достаточна для выхода на гелиоцентрическую орбиту. При этом мы рассматриваем траекторию от начальной точки, которая в момент
удалена от Земли на 0,5 — 1 млн. км, что практически исключает гравитационное торможение. Относительная скорость, которая требуется для ухода с околоземной орбиты будет близка к 15 — 16 км/сек. Соответствующий расход топлива в 4 — 5 раз превысит нетто-массу корабля ~350 т. Отсюда получается оценка его стартовой массы на околоземной орбите ~2 000 т. Расстояние от орбиты Земли до Марса в момент прибытия принято равным 58 млн. км.
Начнем с самого быстрого маршрута. При градусов корабль достигнет орбиты Марса через 56 дней. Планета уже должна быть в этой точке, для чего нужно правильно выбрать дату старта. Вот вам и полгода путешествия «туда» )) Однако, не спешите вылетать! В этом случае скорость прибытия относительно Марса, без учета его тяготения, составит 11,9 км/сек. А с учетом гравитационного разгона она приблизится к 16.9 км/сек. Скорость придется сбросить на 16,9 — 3,6 = 13,3 км/сек, чтобы выйти на околомарсианскую орбиту. Согласно формуле (1) потребуется запас горючего, который в 18.2 раза больше нетто-массы корабля. Если последняя равна 100 тонн, то к моменту начала торможения он должен иметь массу около 1 800 т. Поскольку для с перехода с низкой околоземной орбиты на траекторию полета к Марсу нужно ускориться на
км/сек, потребуется 1 800 т топлива (1). С учетом гравитационного торможения от Земли его расход будет многократно выше. Таким образом, нужно собрать на орбите и загрузить корабль со стартовой массой в несколько раз большей, чем у гигантского Сатурна-5. При этом мы не учитывали топливо для возвращения домой. Самый быстрый полет стал бы самым сложным и дорогим. Поэтому не будем так спешить на Марс!
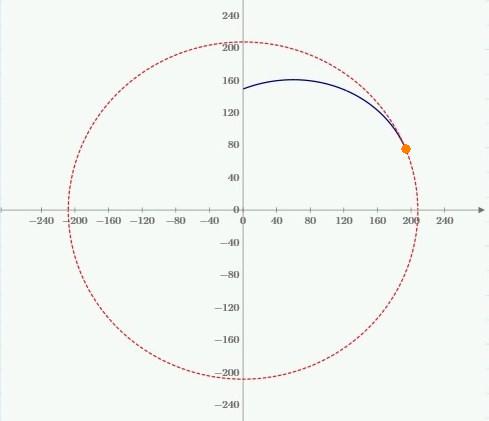
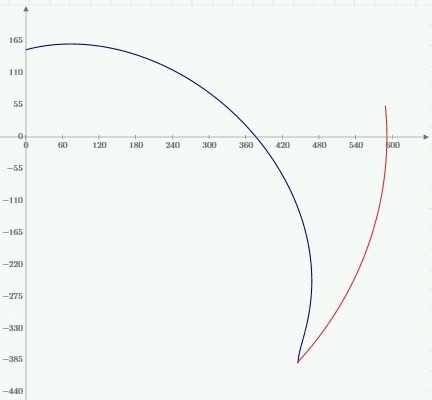
График 1. Траектория полета к Марсу при начальном тангаже 100 градусов.
Близкая к оптимальной траектория полета соответствует углу тангажа градусов. Это означает, что начальный вектор
направлен под углом 10 градусов к вертикали так, что корабль удаляется от центра и движется слегка назад (под вертикалью подразумевается направление радиус-вектора в момент старта, начало координат в центре Солнца). Но речь идет о скорости относительно Земли, которую нужно сложить с орбитальной
(29,78 км/сек), поэтому результирующая скорость корабля относительно Солнца будет направлена так, как на графике 1. Марс в момент прибытия изображен оранжевым кружком. Его радиус-вектор отклоняется на 68,5 градусов от вертикали по часовой стрелке. Отметки координат даны в миллионах км.
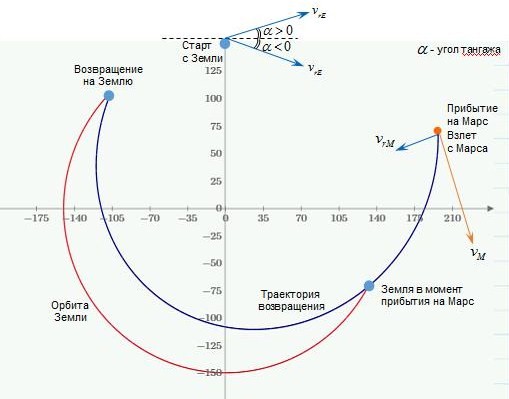
График 2. Траектория полета от Марса к Земле.
Предположим, что экспедиция проведет 4 — 5 дней около Марса. Из них 2 дня на маневрирование и проверку систем по прибытии и подготовку к возвращению, 1 день на высадку и взлет-стыковку с командным модулем, 1 день пребывания на поверхности планеты. Следующий такой полет произойдет не скоро, поэтому было бы неразумно ограничится часами долгожданного свидания с Марсом. В момент выхода на орбиту возвращения к Земле она будет находиться в точке, радиус-вектор которой отклоняется от вертикали на 117 градусов (голубой кружок справа).
Таким образом, за время полета к Марсу наша планета значительно обгонит корабль. Этот маршрут продлится 114 дней — около 4-х месяцев. При этом скорость относительно Марса к моменту прибытия составит 4,1 км/сек без учета гравитационного разгона. Чтобы понять, какими будут затраты топлива на торможение, необходимо принять его во внимание. Марс способен ускорить корабль на 5 км/сек, но не больше этого. Закон сохранения момента импульса поможет нам оценить его влияние. Пусть — начальная скорость корабля относительно Солнца, т.е.,
. Вектор его скорости в момент прибытия к Марсу разложим на радиальную и касательную компоненты, так что
.
Момент импульса корабля относительно начала отсчета в течение полета от Земли до Марса остается неизменным. Это имеет место от выключения двигателей разгона до начала торможения, если не учитывать гравитацию планет. Что касается Земли, то с достаточной для нас точностью ее можно игнорировать, считая, как сказано выше, что корабль выходит на траекторию полета к Марсу, будучи на расстоянии 0.5 — 1 млн. км от нашей планеты (имея при этом относительную скорость 11,2 км/сек). Гравитацию Марса можно игнорировать до тех пор, пока корабль не приблизится на расстояние ~1 млн. км. После этого он начнется испытывать гравитационный разгон, что приведет к увеличению скорости на 5 км/cек, но заметно проявит себя лишь на удалении порядка 200 тыс. км от Красной планеты.
Таким образом, на рассматриваемом участке траектории момент импульса корабля можно считать постоянным. Отсюда следует, что
(3)
где км/cек — начальная скорость относительно Земли. Используя (3), поскольку скорость прибытия относительно Марса
км/сек, получаем
км/сек и
км/сек.
Докажем, что, без учета гравитации планет, при старте от Земли с 2-й космической скоростью в момент прибытия к Марсу относительная скорость корабля не может быть меньше 4,06 км/сек. Для этого нужна формула (3), выражающая закон сохранения момента импульса, а также закон сохранения энергии:
(4)
Здесь обозначает массу Солнца, так что правая часть (4) равна -493,54 (км/сек) в квадрате. Из (3) и (4) следует выражение скорости корабля относительно Марса в момент пересечения его орбиты:
(5)
Из условия вытекает следующее неравенство:
,
которое равносильно . Подставляя в (5) граничное значение
получим минимально возможное
км/сек. Ему соответствует начальный угол тангажа
градусов, выбранный выше для оптимальной траектории полета к Марсу. Стоит заметить, что представленные формулы можно использовать для выбора оптимальной по скорости прибытия траектории для любого значения начальной относительной скорости
.
Теперь пора вспомнить о том, что у Марса есть гравитация, поэтому к относительной скорости корабля он добавит cвои 5 км/сек. Таким образом, для выхода на низкую околомарсианскую орбиту нужно будет сбросить скорость на км/сек. Согласно (1) потребуется запас топлива, который близок к 2,5 нетто-массам корабля. При этом потребности спускаемого аппарата и возвращения на Землю будут обеспечены танкером, отправленным заранее в автоматическом режиме.
Спуститься-подняться на Красную планету трудней, чем на Луну из-за в 2,3 раза большей гравитации. Давление у поверхности близко к давлению на высоте 35 км над Землей http://www.digitaldutch.com/atmoscalc/ (около 600 Па). Боеголовки МБР тормозят примерно там и выше http://extremal-mechanics.org/archives/9573. Это означает, что атмосферу Марса можно эффективно использовать для торможения спускаемого аппарата, если удастся избежать столкновения с рельефом (там есть высокие горы, в т.ч. выше 20 км). Спускаемым аппаратам 4-х марсоходов это удалось.
Здесь необходимо принять во внимание гравитационные потери скорости, поэтому топлива для посадки и взлета потребуется больше, чем дает формула (1). Первая ступень Сатурна-5 была способна развить 3,6 км/сек, что равно 1-й космической скорости Марса, но теряла на гравитацию 1,2 км/сек. На Марсе она бы потеряла в 2,6 раза меньше, т.к. импульс силы тяжести Земли больше в 2,6 раза (отношение ускорений свободного падения). Исходя из этого, для взлета с поверхности и выхода на круговую орбиту потребуется около 4 км/сек. Тогда формула (1) дает оценку расхода топлива в 150% от массы аппарата. Современные материалы позволят сделать более легкий спускаемый модуль, чем те, которые садились на Луну. По-видимому, массу пустого марсианского модуля можно оценить в 5 — 6 тонн. С учетом аэродинамического торможения, его начальный вес составит около 30 тонн, что вдвое больше лунного модуля Аполлонов. Для упрощения задачи следует ограничиться высадкой одного космонавта, оставив второго в командном модуле. Это разумно и в отношении безопасности миссии в целом. Компанию первому человеку, ступившему на Марс, составят мотороботы.
Для возвращения на Землю следует покинуть Марс под углом -90 градусов к его орбите (см. выше график 2), имея относительную скорость км/сек. С учетом потерь на гравитационное торможение, на околомарсианской орбите нужно ускориться от 3,6 км/сек до 8,9 км/сек, т.е.,
км/сек. Для этого потребуется примерно 230 т топлива, которое будет заранее доставлено автоматическим кораблем — танкером. Через 200 дней полета командный модуль вернется на Землю, имея относительную скорость 11,1 км/сек без учета земной гравитации. Последняя добавит еще 11,2 км/сек (2-я космическая скорость), и это ускорение станет заметным на расстоянии ~1 млн. км от Земли. Как видно, возвращение происходит почти симметрично началу экспедиции. Для выхода на околоземную орбиту пришлось бы сбросить скорость на 14,4 км/сек. Запаса топлива для этого уже не будет, поэтому можно рассчитывать только на аэродинамическое торможение.
Для того, чтобы уменьшить чудовищный нагрев при скорости входа в атмосферу 22,3 км/сек, можно было бы тормозить в два этапа. Сначала пройти по касательной так, чтобы замедлиться до меньше, чем 11,2 км/сек. Поскольку аналогичное торможение удалось осуществить в рамках программы Аполлон, нет сомнений в том, что его можно выполнить под меньшим углом входа в атмосферу, который обеспечит выход на эллиптическую орбиту. Корабль (точней спускаемая капсула, т.к. все остальное сгорит) приблизится к Земле на 20 — 30 км и снова уйдет в космос. С этой орбиты капсула сойдет на втором этапе торможения, поэтому экипажу придется еще несколько дней ждать приземления. Впрочем возможно, что двухступенчатое торможение не понадобится и корабль сбросит скорость до нуля при первом вхождении в атмосферу. При этом выделится в 4 раза больше тепла, чем при торможении капсул Аполлонов.
Заметим, что траектория возвращения на Землю приближается к орбите Венеры и даже проходит чуть ближе к Солнцу (график 2 выше). Это обещает дополнительные, волнующие возможности, хотя и несколько осложняет радиационную защиту. На орбите Венеры уровень солнечной радиации примерно в 2,2 раза выше, чем на орбите Земли. Это отнюдь не выглядит критичным, а если торчать полтора года на Марсе в ожидании противостояния, то суммарная доза радиации может оказаться большей. Отдельного изучения заслуживает вопрос: возможно ли организовать марсианскую миссию так, чтобы на обратном пути встретиться с Венерой?
ВЫВОДЫ
1. Используя актуальные ракетно-космические технологии, основанные на ЖРД, можно достичь Марса за 4 месяца, высадиться на планету и пробыть там несколько дней, после чего за 6,5 месяцев полета вернуться на Землю.
2. При выходе с 2-й космической скоростью (11,2 км/сек) на траекторию полета к Марсу, которая оптимальна с точки зрения расхода топлива на торможение, угол тангажа составляет 100 градусов.
3. Такая экспедиция может быть осуществлена с помощью корабля, собираемого на околоземной орбите и имеющего стартовую массу ~2 000 тонн. Из них ~1 600 т придется на топливо и окислитель для выхода на траекторию полета к Марсу, ~250 т для торможения и маневрирования по прибытии. Около 230 т топлива для возвращения на Землю и ~25 т в спускаемом аппарате с полной массой ~30 т должны быть заранее доставлены на околомарсианскую орбиту транспортным кораблем.
Таким образом, пилотируемая экспедиция на Марс является не таким сложным делом, как принято думать. Использование ЖРД для этого — далеко не лучший, но пока единственно доступный вариант. Намного больше для марсианской миссии подходят ядерные двигатели с теплоносителем (ЯРД), которые способны дать вдвое больший удельный импульс и были давно проверены в рабочих образцах.
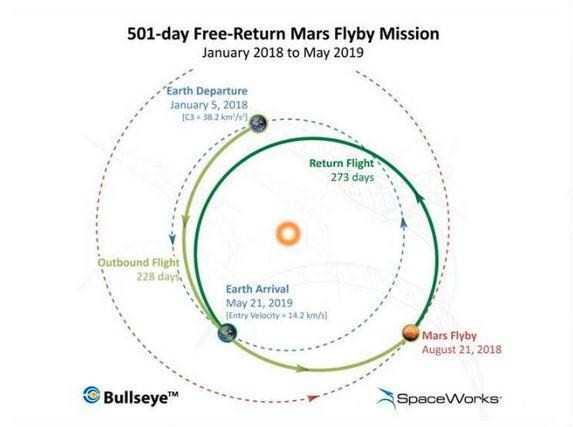
После такого обилия математики можно развлечься, почитав о планах частного фонда Inspiration Mars отправить влюбленную пару в облет Марса за 501 день http://www.space.com/19981-private-mars-mission-married-2018.html. Предлагается просто пролететь мимо Красной планеты, полюбовавшись на нее из иллюминатора. С технической точки зрения эта идея сравнительно легко осуществима. Корабль выходит на траекторию полета к Марсу со скоростью ~8,4 км/сек относительно Земли (заметно меньше, чем выбранные выше 11,2 км/сек). Через 228 дней он достигает Марса и еще через 273 дня возвращается к Земле с относительной скоростью 14,2 км/сек. Наиболее серьезная проблема данного проекта — обеспечение радиационной защиты экипажа, которых уместно назвать путешественниками. На мой взгляд, такая развлекательная миссия дискредитирует Великую Идею, а без высадки на поверхность Марса полет к нему теряет вдохновляющее содержание. При этом симптомы лучевой болезни, которые проявятся через несколько месяцев, сделают его тяжелым испытанием. Полет на Марс — это подвиг, а не романтическое путешествие!
QUOD LICET JOVI NON LICET BOVI
В шедевре Кубрика и Кларка, снятом в далеком 1968, Космический Одиссей прибывает к Юпитеру, чтобы продолжить свое путешествие через гиперпространство. Проход в которое непостижимым образом открыл загадочный монолит. В то время еще не было известно, насколько страшным местом являются окрестности гиганта, собравшего больше 70% массы всех планет Солнечной системы. Юпитер, наполненный жидкометаллическим водородом, обладает могучим магнитным полем и, как следствие, чудовищными радиационными поясами. Статья, в которой агитпроп о будущем российском зонде «Лаплас» (что помешало провести хоть одну миссию в глубоком космосе за 15 лет купания в нефтедолларах?) сочетается с интересным материалом о радиации в окрестностях Юпитера http://zoom.cnews.ru/rnd/news/top/na_puti_k_evrope_vstayut_barery_iz_radiatsii/print.
Монолит на орбите Юпитера, скриншот из «2001: A Space Odyssey»
На орбите вблизи поверхности, допустим ~30 000 км (радиус планеты около 70 тыс. км), за сутки можно получить ~10 000 рад = ~100 грэй даже через 2 см алюминиевой обшивки. Космический Одиссей прожил бы в таких условиях лишь несколько мучительных часов, т.к. ~1 грэй вызывает лучевую болезнь, а одноразовая доза в 10 грэй влечет мгновенную смерть. На самом деле все еще хуже! Протоны с энергиями в десятки Мэв, которых много в радиационных поясах Юпитера, могут увеличить эквивалентную дозу облучения до 20 раз (т.е. до ~ 2 000 зивертов за сутки). Сомнительно, что человек в кабине без массивной биозащиты протянет там хотя бы час. Но дальше от планеты еще интересней. На расстоянии ~100 тыс. км можно получить в 10 раз больше радиации, а через слой аллюминия в 1 мм — такими пластинами можно усилить защитные свойства скафандра — еще 10-кратно. Космонавт, высадившийся на поверхность Ио или самого интригующего спутника Европа, умрет почти мгновенно. Даже без радиации, вулканически гиперактивная Европа — не лучшее место для прогулок. Намного удобней в этом смысле Ганнимед, который больше Луны в 1,5 раза и имеет расплавленное, железное ядро. Удаленный на 1 млн. км от Юпитера, он также ощущает действие этого «ускорителя» заряженных частиц. На поверхности Ганнимеда космонавт за 1 час получит ~0.5 грэй, а биологически эквивалентная доза будет в разы больше. Это — гарантированная лучевая болезнь. На Каллисто, которая удалена на 1 870 тыс. км, ситуация несколько лучше, но и там разгуливать больше получаса противопоказано.
Таким образом, из 4-х крупных спутников только Ганнимед и Каллисто годятся для относительно безопасной высадки, … если никто не покинет спускаемый аппарат больше, чем на несколько минут, а у него массивная биозащита. Но эти планеты далеко от Юпитера, а лететь к нему через толщу радиационных поясов чревато. Автоматический зонд «Галилео» при сближении с чудовищем получил дозу радиации, которая в ~25 раз превышает смертельную для человека. Условия работы в окрестностях Юпитера являются экстремальными даже для электронного оборудования! Бронированный достаточной биозащитой корабль будет слишком тяжелым, хотя создать его теоретически возможно. По-видимому, с намагниченным монстром лучше общаться на расстоянии, используя роботов в качестве посредников. Этим успешно занимается NASA в гордом одиночестве, отправив на встречу с ним зонды Пионер 10 и 11, Вояджер 1 и 2, Галилео и Кассини.
Тем не менее, интересно оценить техническую возможность пилотируемого полета к Юпитеру, используя современные возможности. Мы не будем глубоко вдаваться в этот вопрос, ограничившись моделированием траектории в один конец. Противостояния Юпитера повторяются почти через 13 месяцев, ближайшее Великое противостояние 26 сентября 2022. Однако, из-за небольшой эллиптичности орбиты разница минимальных расстояний между Землей и Юпитером относительно невелика — 62 млн. км (эти расстояния не могут быть меньше 591 млн. км). Поэтому дату вылета на встречу с чудовищем можно выбирать ежегодно. На первый взгляд, 10-кратная разница с минимальной дистанцией до Марса требует значительно большей скорости полета. Но, как ни странно, это не так. Решалась система уравнений, которая учитывала мощную гравитацию Юпитера:
(6)
где — масса Юпитера,
млн. км — радиус его орбиты в момент Великого противостояния,
— угловая скорость планеты,
— угол между направлениями от Солнца к Земле и Юпитеру в момент старта корабля. Как и выше предполагается, что в момент
Земля находится на положительной полуоси Y. Начальные условия выбирались те же, что в задаче (2), но с несколько большей начальной скоростью
км/сек относительно Земли. По причинам, которые изложены выше (2), расчет велся до точки траектории, удаленной от Юпитера на ~1 млн. км. От нее «до планеты» оставалось еще около 10 узлов расчетной сетки, что позволило избежать последствий сингулярного поведения системы (6) вблизи точки, где знаменатель второго слагаемого обращается в ноль. Таким образом, расчет траектории велся до места, удаленного от Юпитера примерно также, как его спутник Ганнимед. Можно считать, что моделировался полет до Ганнимеда для высадки на его поверхность.
График 3. Полет к Юпитеру за 560 дней.
При начальной относительной скорости 12 км/сек и угле тангажа градуса за 560 дней полета будет достигнута точка, удаленная от Юпитера на 940 тыс. км. Таким образом, собранный на околоземной орбите корабль способен за 1,5 года прибыть к Ганнимеду. Относительная скорость прибытия составит 13,3 км/сек при орбитальной скорости планеты 10,9 км/сек. С учетом гравитационного разгона от Ганнимеда на 2,7 км/сек (2-я космическая скорость), для выхода на низкую круговую орбиту нужно сбросить скорость на 13,3-10,9+2,7-2=3.1 км/сек. Здесь 2 км/сек — скорость на орбите вокруг планеты. В силу формулы (1), торможение потребует затрат топлива, примерно равных нетто-массе корабля. Однако, поскольку в момент прибытия он окажется ближе к Юпитеру на ~100 тыс. км, гравитация гиганта обеспечит дополнительное торможение. Учитывая ускорение при выходе на траекторию возвращения запас топлива, который должен оставаться после разгона от Земли, не превысит 3 нетто-массы. Как и в случае полета на Марс, топливо на обратную дорогу следует заранее отправить автоматическим танкером. С учетом дополнительной, весьма серьезной биозащиты масса корабля без топлива составит 200 — 250 тонн.
Но нельзя ли сократить время полета? Можно! Например, при начальном угле тангажа , т.е., при уходе от Земли в направлении касательной к ее орбите время полета сокращается до 350 дней — почти год. Но, как и в случае с Марсом, за это приходится платить относительной скоростью прибытия. В точке, удаленной от Юпитера на 980 тыс. км, она составит 21,8 км/сек, что принципиально усложняет задачу торможения для высадки на Ганнимед.
Итак, на графике 3 изображена технически разумная траектория полета от Земли к Юпитеру за 560 дней (синяя линяя). Красная линяя изображает траекторию его движения от момента старта корабля до прибытия на Ганнимед. Видно, как могучая гравитация Юпитера изгибает траекторию полета за десятки млн. км от места встречи. Высадка на поверхность Ганнимеда будет немногим более сложной задачей, чем на Луну, т.к. их гравитационные поля мало отличаются.
Таким образом, мы приходим к поразительному выводу о том, что пилотируемый полет с посадкой на Ганнимед организовать принципиально не сложнее, чем на Марс, хотя риск для здоровья экипажа будет многократно выше. При этом массу корабля при выходе на траекторию к Юпитеру можно удержать в пределах 400 — 500 тонн, придав ему скорость относительно Земли 12 км/сек. Выигрыш в полезной нагрузке за счет меньшего запаса топлива на торможение по прибытии составит ~100 т, что можно потратить на биозащиту. Стартовая масса на околоземной орбите ~2 000 — 2 500 т, из которых ~1 600 — 2 000 т придется на топливо для ускорения при уходе с околоземной орбиты на траекторию полета (график 3)
 Эскизный проект ядерного марсолета NASA
Эскизный проект ядерного марсолета NASA
Итак, уже сегодня можно организовать пилотируемую экспедицию к Юпитеру с посадкой на Ганнимед при почти тех же технических усилиях и материальных затратах, как на Марс. Этот полет продлится 1.5 года туда и примерно столько же обратно. Поэтому необходимо решать проблему искусственной гравитации. Пример того, как это может быть реализовано, показан в фильме Interstellar http://extremal-mechanics.org/archives/15798. Для экономии жизненных ресурсов и снижения массы биозащиты следует ограничиться экипажем из двух человек. Один из них высадится на поверхность Ганнимеда, чтобы установить там флаг, совершить прогулку и т.п., имея лишь несколько минут на волнующие ритуалы, которые останутся в истории навечно. Затем придется быстро покинуть опасную планету и укрыться за основной биозащитой командного модуля. Для возвращения к Земле возможен гравитационный маневр с максимальным приближением к Юпитеру, который выглядит очень заманчиво, но предъявляет высокие требования к биозащите корабля.
Мы снова возвращаемся к необходимости создания ракеты с ЯРД, которая позволит выполнить пилотируемую миссию на Марс или к Юпитеру с намного меньшими усилиями, большим уровнем комфорта и безопасности для экипажа. В частности, отпадет необходимость в оправке танкера с горючим на обратную дорогу. Кроме того, существенно сократится время полета к Юпитеру и откроется дорога к таинственному Сатурну, который находится вдвое дальше от Земли http://www.vokrugsveta.ru/vs/article/570/. Магнитное поле этой планеты намного слабей, чем у Юпитера, поэтому она значительно безопасней с точки зрения радиации. Если уж отправляться в дальний путь, то лучше сразу туда. Но только на корабле с ЯРД! В заключение стоит заметить, что автор романа «2001: Космический Одиссей» Артур Кларк отправил своего героя не к Юпитеру, как в фильме Стэнли Кубрика, а к Сатурну.
Дмитрий Зотьев
продолжение этой темы до Сатурна в новой статье http://extremal-mechanics.org/archives/22067.





Материал этой статьи является во многом эксклюзивным. Реалистичный план экспедиции на Марс быстрей, чем за 1 год. Принято думать, что на такой полет уйдет 2 — 2,5 года. Второй неожиданный вывод заключается в том, что пилотируемый полет к Юпитеру сравним по сложности с миссией Марс. Если не учитывать фактор радиации, которая вблизи гиганта запредельная!
Cенсационная лекция о том, что на Венере, может быть, есть развитая жизнь. Гипотеза основана на снимках этой планеты, полученных советскими зондами Венера-13 и 14 в те времена, когда наша страна была способна на большее, чем проведение чемпионатов мира по футболу. Крайне интересно, хотя смущает тот факт, что фотографии подверглись компьютерной обработке, которая могла исказить детали исходных изображений. Это стоит посмотреть и послушать ))
В потрясающем романе Кларка «Космическая Одиссея 2001″, который лег в основу киношедевра Кубрика, есть эпизод, которого нет в фильме. А именно, корабль «Дискавери» проносится мимо Юпитера по касательной, и экипаж (Дэйв с Фрэнком) взолнованно рассматривают в иллюминатор бездонные глубины атмосферы гиганта, мелькающие в просветах облаков.
Столь близкое свидание с Юпитером, продолжавшееся несколько часов, в реальности было бы невозможно из-за чудовищной радиации вблизи этого монстра. Экипаж «Дискавери» погиб бы от облучения в течение считанных часов, и корпус корабля его не спас бы. В то время, когда Артур Кларк писал свой роман (вторая половина 60-х) об этом еще не было известно ничего.
В романе корабль благополучно покинул Юпитер, продолжив свой путь к Сатурну. Статья о том, как можно было бы осуществить такое путешествие в наше время http://extremal-mechanics.org/archives/22067.
Тут поступило предложение отправить телескоп на 500 а.е. от Солнца!
https://www.gazeta.ru/science/2016/10/17_a_10254449.shtml
Спасибо, очень интересный материал!
Идея красивая и, вероятно, реалистичная. Но отправить на 500 а.е. телескоп быстро на получится. Автор ссылается на «Вояджер», пролетевший 130 а.е. за 40 лет и утверждает, что есть технологии, позволяющие проделать этот путь гораздо быстрее. Но таких технологий нет, насколько я могу судить. Лет 100 пройдет в лучшем случае, пока он туда доберется, если использовать существующие методы космического движения. Сократить время хотя бы до 20 лет, чтобы сделать проект привлекательным, чрезвычайно трудно. Нужны прорывные решения, например реанимировать проект «Орион». Хотя толчки от ядерных взрывов при разгоне телескопу вряд ли понравятся. А так здорово придумано ))
Стоит ли овчинка выделки? Допустим этот трюк добавит 26 звездных величин к якости планеты около Альфа-Центавра b. Очевидно, что ее звездная величина хорошо за 30. Будет наблюдаема таким удаленным телескопом, допустим, как объект 6 — 10 величины. Видимый угловой размер будет все равно ничтожный. Что там можно будет разглядеть? Ничего мне кажется. Разве лишь получится хороший спектральный анализ. Это конечно ценный результат, но оправдает ли он такой мегапроект? Не факт. Впрочем, все мои доводы навскидку. Нужно оценивать, чтобы судить об этом.
По-моему наличие планеты в системе Альфа-Центавра надежно не подтверждено. Но если она там есть, то нужно срочно к ней лететь )) Система чрезвычайно интересная, вот только лететь туда не на чем.
Я знал, что вам понравится. В статье было заявлено увеличение 1E+11, я думаю, это неточность журналиста, скорее всего имелся ввиду дифракционный предел по углу 1E-11 радиан. Если так, то это даёт разрешающую способность 380 км на расстоянии 4 световых года. Если у Альфа Центавра есть планета земного диаметра, её изображение будет иметь примерно 30 пикселей в поперечнике. На мой взгляд маловато, надо бы еще на порядок поднять, чтобы было 300 пикселей. Но может телескоп потянет и 1E-12? Тогда будет сенсационное качество изображения. С другой стороны, гравитационная линза, насколько я понимаю, фокусирует далеко не в точку, а имеет хитрые аберрации. Это усложняет задачу. Но НАСА вроде бы и даёт деньги на предварительную проработку реализуемости проекта. Это уже неплохо.
Всё таки, согласитесь, что это тот проект над которым хотя бы можно начать работать. В отличие от межзвездного корабля, который просто невозможно построить ни сейчас, ни в перспективе ближайших десятилетий. А пролететь 500 а.е. несколько проще, чем 200 тысяч а.е.
Безусловно! Проект весьма вдохновляющий, в том числе в плане разработки новых технологий космического движения. С аберрациями можно разобраться, чем этот парень собственно и занимается. Насчет разрешения нетрудно оценить. Расстояние от Земли до этого телескопа в 400 раз меньше, чем от него до Альфы-Центавра. Диаметр Солнца больше земного в 100 раз. Значит угловое разрешение увеличится в 400*100 = 40 000 раз, чем если наблюдать с Земли (считаем, что с аберрациями разобрались). Тогда угол наблюдения диаметра земной орбиты составит грубо 50 000 угловых секунд (из расчета 1 сек на 3.26 световых года = 1 парсек), т.е., около 13.5 градусов. Очень много!
Но что касается планеты, допустим земного размера, то она будет видна под углом грубо в 4 000 раз меньшим, т.е., чуть больше 10 секунд. Это на 2 порядка выше дифракционного предела «Хаббла». Грубо — половина углового размера Марса. Так что кое-что удастся разглядеть )) Стоит заметить, что угловой размер половина Марса — это для телескопа. Так что теоретически на планете можно будет разглядеть детали рельефа, как на Марсе. 380 км запросто! Но опять же, аберрации сильно ухудшат качество картинки. И все-таки … Вы правы, этим есть смысл заниматься
Вот только один момент меня смущает. Можно ли разглядеть свет, отраженный планетой в системе Альфа Центавра на фоне солнечного света, который будет интенсивней в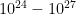 раз? (очень грубая оценка, основанная на сравнении звездных величин). По идее, любая оптика должна быть «засвечена». То есть, достаточно чувствительные элементы не смогут работать при свете Солнца. Подобно тому, как астронавты на залитой солнечным светом Луне не могли увидеть или сфотографировать звезды, что дало повод для безграмотных измышлений конспирологов.
раз? (очень грубая оценка, основанная на сравнении звездных величин). По идее, любая оптика должна быть «засвечена». То есть, достаточно чувствительные элементы не смогут работать при свете Солнца. Подобно тому, как астронавты на залитой солнечным светом Луне не могли увидеть или сфотографировать звезды, что дало повод для безграмотных измышлений конспирологов.
Как эту проблему решать предполагается? Наверное собираются спектральные светофильтры ставить, чтобы «потушить Солнце». Но ведь обе звезды в системе Альфа-Центавра имеют близкий к Солнцу спектр. Тоже касается системы Тау-Кита, которая крайне интересна на предмет наличия там жизни http://extremal-mechanics.org/archives/1428. По-видимому, такой метод применим только к разглядыванию планет около звезд другого класса (гигантов, карликов или горячих звезд). Хотя не факт, что можно эффективно отфильтровать свет с интенсивность на 24 или более порядков выше (если верна моя оценка, разумеется). В общем, здесь все не так просто с точки зрения физики … даже до инженерной реализации данного проекта.
Гравитационная линза сфокусирует свет планеты и поднимет её яркость во много раз, думаю, на порядки. Диск Солнца придётся закрыть маской. Надо считать коэффицент усиления.
Это зависит от того, на каком расстоянии от Солнца будет действовать гравитационная линза. Если на порядка размера его короны, то наверное будет так, как Вы говорите. Мне представляется, что линзируемые лучи должны быть близки к краю солнечного диска (без короны). И тогда существенно повысить относительную яркость не получится. И если закрыть маской солнечную корону, то на таком удалении от Солнца, наверное, исчезнет и линзирование. Лучи ведь должны достаточно близко пройти от него, чтобы быть искривленными. Но возможно, что я ошибаюсь насчет размеров линзы.
Можно сделать такую оценку усиления. Максимальное отклонение луча света в гравитационном поле Солнца происходит у самой его границы и составляет примерно 1.75″. Радиус Солнца 700 тыс.км. отсюда находим расстояние до ближайшего фокуса равное 550 а.е. Разместим там телескоп диаметром 1.4 м. . Это соответствует усилению на 22.5 звездных величин.
. Это соответствует усилению на 22.5 звездных величин.
Теперь мысленно разместим такие же телескопы вдоль окружности Солнца. Таких телескопов там поместится миллиард штук. Значит коэффициент усиления солнечной линзы для такого телескопа в точке ближайшего фокуса 550 а.е. будет около
Опечатку я исправил. Рассуждение Ваше остроумно, но если отклонение луча происходит у края солнечного диска, то оттуда же к телескопу придет свет от Солнца и ослепит его (о чем я и писал). Закрыть край Солнца маской не получится, т.к. есть еще корона. Дифракция от края маски опять же. Поэтому мне кажется, что для работоспособности такой системы гравитационная линза должна отклонять лучи значительно дальше от Солнца, ну скажем за 2 млн. км от его центра.
В усиление на 22.5 величины я вполне верю, даже на 26, как сказано в статье. Но дело в том, что даже после этого свет от экзопланеты останется на 30 или больше звездных величин слабее солнечного. Поэтому смешивать его с солнечным светом никак нельзя. Мне кажется, что линза должна преломлять свет от планеты не у края солнечного диска, а гораздо дальше, за пределами короны. Тогда получится экранировать телескоп от Солнца. Хотя дифракция от краев экрана все равно останется, но этот свет будет значительно слабее (нужно считать). К тому же можно сделать экран из светопоглощающего материала дабы снизить дифракцию. Так что, наверное, с ней можно разобраться.
Телескоп Хаббл имеет рабочую чувствительность около 28m.
В точке солнечного фокуса чувствительность будет 28+22=40m
Неплохо на мой вгляд.
Дифракционный предел солнечного телескопа должен вычисляться как и для обычного = лямбда/Dсолнца. Что даёт примерно 10^-15. С таким предельным углом можно рассматривать планеты даже на расстояниях в тысячи световых лет. Поэтому про дифракционный предел можно забыть и в расчетах ограничиться геометрической оптикой. Это плюс.
Конечно, перспектива такого телескопа выглядит крайне заманчивой, если удастся экранировать его от Солнца. Хотя насчет разглядывания планет за тысячи парсек я бы не торопился. Там же дело не только в дифракционном пределе. За тысячи световых лет звездные величины возрастут еще на 10 — 12 единиц, а угловые размеры уменьшатся до порядка десятой доли секунды (на входе в телескоп). То есть до угловых размеров Плутона, а на нем ничего нельзя разглядеть даже в Хаббл. Увидеть бы для начала планету в Альфе Центавра ))
Если использовать в качестве линзы гравитационное поле на расстоянии около 1 радиуса от поверхности Солнца (2 солнечных радиуса от центра), то фокус будет в 4 раза дальше. Это не годится. Лететь на 2000ае далеко
Звездная величина Солнца (с Земли) -27m. Световой поток Солнца на расстоянии 550 а.е. ослабнет в 550^2=302тыс. раз. Это соответствует ослаблению на 14m. Итого, Солнце будет иметь примерно -13m.
Предположим, что экзопланета похожа на Марс. Максимальная звездная величина нашего Марса с Земли примерно -3m. Это в моменты противостояния. Расстояние до него в этот момент около 0.3 а.е. Если мы сдвинемся к ближайшей звезде на 300 тыс. а.е. (в 10^6 раз дальше) световой поток упадет в 10^12 раз. Это соответствует ослаблению на 30m. Блеск Марса упадет до -3+30=+27m. Но у нас усилитель на 26m! Итого экзомарс будет иметь блеск +1m, а Солнце -13m. Получается, Солнце будет ярче на 14 звездных величин… Мда…
Но есть еще маска. Сможет ли она ослабить центральное светило на 14m?
В общем, надо думать
То есть грубо в 10 млрд. раз нужно ослабить. Маска закроет диск Солнца, но корона останется. Боюсь, что есть только один выход — линзировать лучи подальше от Солнца. А почему Вы полагаете, что на расстоянии радиуса от поверхности Солнца в 4 раза уменьшится угол отклонения лучей? От того, что гравитационный потенциал уменьшится в 4 раза? Но ведь луч пройдет вдвое большее расстояние при повороте, грубо говоря. Значит, если на единицу пройденного пути угол поворота будет в 4 раза меньше, то в итоге луч повернется на в 2 раза меньший угол. Тогда придется тащить телескоп не на 2 000 а.е, а только на 1 000 а.е. Уже легче Хотя корона и там будет слепить наверное. Но гораздо меньше!
Хотя корона и там будет слепить наверное. Но гораздо меньше!
Черная дыра была бы идеальной линзой. Хотя аккреционный диск сияет. Но если он диск, то в плоскости этого диска его можно экранировать. Вот только до ближайшей черной дыры несколько тыс. световых лет. Жаль, что планеты не годятся в качестве гравитационных линз, т.к. фокусы уедут к звездам.
Разница в 14m — это в 400 тыс. раз получается по интенсивности (5m = в 100 раз). Может удастся хитрую линзу Френеля изготовить? Чтобы она за счет интерференции затемняла центр и усиливала ободок вокруг солнечного диска? Но корона, да — это проблема. Кроме её собственного свечения, есть еще опасность, что движение горячего газа в гелиосфере будет искажать волновой фронт проходящих мимо лучей, что вызовет эффект «дрожания» звёзд, как в земной атмосфере. Это ухудшит разрешение солнечного телескопа. Но на сколько? Думаю, придётся тащить коронограф на МКС и делать замеры «дрожания».
Да, угол отклонения уменьшится в 2 раза, но радиус увеличился в 2 раза. Длина фокуса равна радиус делить на угол. В итоге фокус уйдёт в 4 раза дальше.
Еще мне пришло в голову, что ведь экзопланета будет двигаться вокруг звезды, и наш телескоп должен двигаться синхронно, если мы хотим рассмотреть планету в деталях. Сможет ли телескоп так двигаться? Если нет, то придётся выбрать увеличение так, чтобы смотреть сразу на всю орбиту планеты, но тогда не видно будет деталей поверхности и будет слепить звезда. Значит придётся иметь запас топлива. Но наверное можно использовать ионный двигатель, чтобы экономить топливо. За 10 лет ионник может неплохо разогнать. Но надо считать.
На чёрную дыру пока надежды нет Если фокусы планет уезжают к звездам, может мы можем поймать фокус какой-нибудь экзопланеты? Но это другая история.
Если фокусы планет уезжают к звездам, может мы можем поймать фокус какой-нибудь экзопланеты? Но это другая история.
Много уже написал. Пока сделаю перерыв.
Хороших выходных!
Но тогда подозрительно малая разница получается. Согласно Вашим оценкам, разность яркостей Солнца и экзопланеты составляет 56 звездных величин. Пусть гравитационная линза усиливает яркость планеты на 26 звездных величин. Итого имеем разницу на 30. Это означает, что поток света от экзопланеты меньше потока от Солнца в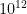 раз. Вы эту разницу уменьшаете до 400 тыс. за счет того, что телескоп отъезжает на 500 а.е. Но ведь звездная величина определяется по наблюдениям с Земли. Поэтому когда авторы проекта заявляют об усилении на 26 звездных величин, то они, очевидно, имеют ввиду именно усиление в
раз. Вы эту разницу уменьшаете до 400 тыс. за счет того, что телескоп отъезжает на 500 а.е. Но ведь звездная величина определяется по наблюдениям с Земли. Поэтому когда авторы проекта заявляют об усилении на 26 звездных величин, то они, очевидно, имеют ввиду именно усиление в 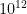 раз. В противном случае они бы заявили об усилении на 56 — 14 = 42 звездных величины.
раз. В противном случае они бы заявили об усилении на 56 — 14 = 42 звездных величины.
Это кстати соответствует Вашей оценке в раз. Вы в ней разместили миллиард телескопов по окружности Солнца. Но если сделать это в 1 000 слоев, то получится моя оценка. Ясно, что гравитационная линза должна фокусировать свет с некоторой области вокруг Солнечного диска.
раз. Вы в ней разместили миллиард телескопов по окружности Солнца. Но если сделать это в 1 000 слоев, то получится моя оценка. Ясно, что гравитационная линза должна фокусировать свет с некоторой области вокруг Солнечного диска.
В общем мне кажется, что отношение интенсивностей света от Солнца и экзопланеты в точке нахождения телескопа будет иметь порядок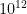 . Если это так, то, наверное, никакие ухищрения с маскировкой Солнца не помогут. Нужно все-таки далеко отодвигать точку нахождения телескопа, как минимум на 2 000 а.е. Может быть тогда получится.
. Если это так, то, наверное, никакие ухищрения с маскировкой Солнца не помогут. Нужно все-таки далеко отодвигать точку нахождения телескопа, как минимум на 2 000 а.е. Может быть тогда получится.
И Вам приятных выходных, хотя они уже прошли наполовину
Через 2 года НАСА отправит на Марс уже 5-й ровер https://news.mail.ru/society/31507401/?frommail=1.
Подумаешь! Зато мы потратили рекордную сумму на Олимпиаду и проведем ЧМ по футболу. Пиндосы обзавидуются. Они только и могут, что отправлять зонды ко всем планетам Солнечной системы ))
Стоит заметить, что СССР посылал автоматические аппараты только к Луне, Марсу и Венере (хотя посадки на Венеру остались непревзойденными). Вставшая с колен Россия не смогла осуществить ни одной миссии за пределами околоземной орбиты в XXI веке. Опять же, нам есть чем гордиться и без космоса: число миллиардеров выросло от 4-х в конце 90-х до 96 сегодня.
Статья в развитие темы об осуществимости пилотируемых полетов к планетам Солнечной системы http://extremal-mechanics.org/archives/22067
Утверждается, что так звучит голос Юпитера, описанный Кларком в романе о Космическом Одиссее. Записывал кто-то из Вояджеров, наслаждайтесь этой психоделикой )) .
проект «Inspiration Mars» — это где-то 500 дней на путешествие.. полетели влюблённой парочкой, вернулись двумя трупами, разорвавшими друг другу глотки
Несерьезная идея. Разорвут друг другу глотки или нет — это неизвестно, хотя вполне могут. Но ясно, что лететь должны идеально подготовленные профессионалы, а не два влюбленных дурачка — туриста. Нельзя профанировать великую мечту человечества! Ну и нельзя посылать людей на Марс без высадки на планету, т.к. их возможные страдания от последствий радиации не будут стоить такого fly-by-я. Увидеть Марс в иллюминатор прямо под собой и не побывать на нем стало бы горьким разочарованием ))
К успешной посадке зонда Insight на Марс. Беседа о состоянии российской космонавтики:
Не услышал почти ничего в ролике о технологической и профессиональной деградации в отрасли, так, мимоходом и опосредованно. Её нет? Сомнительно. Везде есть, и в чудовищном объёме, а там нет. Между тем, чем сложнее квалификация, тем быстрее она теряется, будучи невостребованной.
Ещё один момент: старики вымирают, а есть ли молодые? Эта проблема одна из самых острых везде, куда ни плюнь.
И о деньгах.
Эта типично жлобская логика, согласно которой деньги решают всё, просто невыносима уже. Бесит. Если даже ворьё и жулики, сами привыкшие изымать деньги из чужих карманов, вдруг «зальют деньгами всё что только можно», одно это ничего не изменит. Деньги не заменяют наработанный за всю жизнь опыт, техническую культуру, сплочённый коллектив, ими не заменишь отсутствие специалистов, в качестве мотивации деньги работают только поначалу, а дальше нужно что-то более основательное. Например, дай лично Рогозину хоть триллион долларов, обязав его сдать экзамены за курс технического ВУЗа, ничего у него не выйдет.
Да и крайне сомнительно, что деньги кто-то готов давать. Их повсеместно отбирают, а не дают. Если чьи-то получки и растут, так только топ-менеджеров, а не инженеров, техников и рабочих. Система-то везде одинакова, хоть в колхозе, хоть на космодроме.
Не нашел сходу той ссылки.
По поводу планов.
Планы до 1956 года были контрценностными. 1955-13 миллионов смертей.После смешанными.
Про Макнамару и Кеннеди.
1963.SIOP-63.
1964.SIOP-64.
Макнамара закрыл много программ .Но исследования он не закрыл.Исследование зарядов от 50 МТ до 1 000 000 Мегатонн продолжались до 1978 года.Один из множества примеров.
Планы в 1970-х и 1980-х годах в основном были контрценностными.Першинг-2 c W85 это контрценностная система.Не контрсиловая как писали в » перестройку»
Эти сказки повторяет Сивков. В конце 1940-х -1950-е американская промышленность была способна производить 75 000 танков в год, при мобилизации до 150 000 танков.Что-то здесь Сивков темнит.
По пропаганде.
Советские пропаганд. книги всегда , давали ссылки на источники ( американские и прочие,- газеты, программы партий, слушания и т.д.) и лишь представляли точку зрения СССР.Даже ЦРУ против СССР -несколько сот ссылок.
Путинские пропагандисты, апел. к СССР извращают все это до идиотизма., вплоть о недоступности зарубежных научных журналов в СССР, не политической литературы.Bulletin of the atomic scientists был доступен. Military Balance- часть номеров была в спецхране.Хотя пропаганда КПРФ, Сивкова, Семина и т.д. на самом деле является антисоветизмом.
Тут один важный момент- под империализмом в СССР подразумевались ТНК, не агрессия( это буржуазное понятие империализма).Что делает тот антиамериканизм проамериканской пропагандой в Путинской РФ.Тут другой Путинский холуй Семин,давая ссылку на Washington Post по WW2 придумал наглую ложь.В США написаны тысячи монографий о WW2, никогда там роль СССР не принижалась. Семин плохо понимает американскую систему.Другое дело,что есть разные точки зрения.
Марксизм ( не только то что входило в советский канон) много где преп. в США, были даже теоретики марксизма.Грамши кто в СССР изучал-( на нем была основана идеология PCI).
Резюмируя. В СССР в 1960-1980-х была пропаганда.
В Путинской РФ наглая ложь, абсолютно антиинтеллектульная.Все сводится к тупой ненависти. Я думаю все это очень плохо кончиться.Может быть это наказание Истории.
Прекратить все космические проекты до остановки войн, вооружённых конфликтов, терактов, голода, обеспечения водоснабжения, перевода человечества на энергию Тесла, Б. В. Болотова, магнитного, гравитационного движения, единого законодательства планеты Земля Конституции Планеты Земля на основе Пятидесяти Двух Божьих Заповедей, молитве Господу, молитве человеческой расе с отменой казней и пыток и восстановления экосистемы планеты Земля.
Надо иметь совесть, порядочность, человечность, доброту, ответственность.
С добротой и любовью.
Управляющий Планеты Земля.
Ценёв Геннадий Анатольевич.
Интересное видео о марсоходе Opportunity, Стоит обратить внимание на одну деталь: этот аппарат доставила к Марсу ракета Delta-4, которая не использует российский ЖРД. К вопросу о «зависимости» США от России в ракетных движках, который детально рассмотрен в статье http://extremal-mechanics.org/archives/26200.
В этой статье и в «Цель-Сатурн» вы касались проекта пилотируемого полета на Марс. На 2021 год SpaceX провели уже 7 испытаний Starship и значительное количество испытаний Raptorов.
Мне кажется, ребята очень целеустремленно и настойчиво работают.
Возможно, у Вас появится время, чтобы прокомментировать данный проект с учетом обновленных?
Извините за вмешательство. .
.
Ребята очень целеустремленно работают. Это точно.
Маск работает по 18 часов в день, и требует того же от своих инженеров (сверхурочных). Он считает что настоящий специалист должен работать и в выходные. Да так собственно все работали настоящие люди. От фон Брауна до Королева.
А вообще жалко, что не все знают какую ведущую роль в прорывах (прошлых и будущих) Маска сыграла наша великая страна! Как пишет биограф Маска, после моральной оплеухи в Москве он сказал «Я сам сделаю это» (имея ввиду космич. ракету) после того как его обозвали «фантазером» и указали на дверь в НПО им. Лавочкина и «Космостарте» (Роскосмос). Пожлобились взять 4 млн. долларов за две РС-20 (переделка в Днепр») (наши жлобы хотели 8 млн. содрать). Не дали Маску побаловаться и запустить мышей на Марс. В результате запустили только 22 «Днепра», а остальные 128 шт….РС-20 распилили на металл. Все эти 150 шт. хотели «уничтожить запуском». Обиделся Маск, забыл со злости про свои хотелки богатого самодура о «марсианских мышах» и улетел восвояси поклявшись отомстить…:)
Месть удалась. Наша роль в нашем же позоре неоспорима
Интересно работает ли мордастый Рогозин по 18 часов в сутки? И его банда прихлебателей «эффективных манагеров» расставленных на всех местах (НА ВСЕХ!!) где требуется….завалить все нажитое трудом народа СССР при очередях за элементарной колбасой? Про недвижимость Рогозина все известно, а вот про …..работу…неизвестно ничего кроме толстых надутых щек и наглого вранья.