 Рис. 1 Испытание композитной опоры на прочность
Рис. 1 Испытание композитной опоры на прочность
С начала XXI века опоры ЛЭП из стеклопластика (композитные опоры), активно применяются вместо железобетонных и стальных. Они отличаются значительно большей гибкостью, вследствие чего прогноз искривленной формы таких опор имеет важное значение. Согласно п. 2.5.139 ПУЭ [1]: «расчет опор гибкой конструкции производится по деформированной схеме (с учетом дополнительных усилий, возникавших от весовых нагрузок при деформациях опоры, для первой и второй групп предельных состояний)». Но на практике, а также в научных работах опоры ЛЭП порой считают с учетом только горизонтальных сил [2]. Очевидно это связано с тем, что расчет прогибов железобетонных стоек имеет отчасти символическое значение. В отличие от них композитные опоры могут заметно прогибаться от весовых и ветровых нагрузок.
Мы рассматриваем только одностоечные опоры, которые представляют собой консоль с защемленным концом. В фундаментальной книге [3] дана методика расчета, которая соответствует ПУЭ [1], но ориентирована на железобетонные стойки. В энергетике принято рассматривать собственную тяжесть опоры ЛЭП, а также ледовую и ветровую нагрузки на ее стойку, как сосредоточенные силы, приложенные в центре по высоте [2]. При вычислении прогибов такой подход не создает больших погрешностей, но искажает эпюры напряжений и изгибающих моментов. Последнее, впрочем, не имеет практического значения, если опора не работает в опасной близости от предела прочности. Легко адаптировать методику из [3] для расчета прогибов композитных опор, при котором распределенные по высоте нагрузки учитываются без грубо упрощающих предположений.
 Рис. 2 Схема нагружения опоры из статьи [2].
Рис. 2 Схема нагружения опоры из статьи [2].
Начнем с классического метода расчета прогибов железобетонных опор, следуя [3] и ссылаясь на формулы из этой книги. Пусть на опору высотой действует система горизонтальных сил
и вертикальных сил
, приложенных на уровнях
(считая от земли), где
. Точки приложения сил могут быть смещены по горизонтали от оси опоры. Если на некотором уровне приложены несколько сонаправленных сил, то их можно считать за одну, равную сумме этих сил и приложенную на оси опоры.
При этом следует учитывать изгибающие моменты от эксцентриситетов вертикальных сил. Слово «эксцентриситет» обозначает отличие от нуля суммарных моментов вертикальных сил относительно данной точки. Грубо говоря, весовые нагрузки не сбалансированы. При наличии изгибающих моментов от эксцентриситетов следует принимать их во внимание, заменяя вертикальные силы на одном уровне одной силой, приложенной к оси опоры (см. пример в п. 4.1). С учетом сказанного в дальнейшем предполагается, что на каждом уровне приложена только одна пара сил
.
Расчет прогибов железобетонной, одностоечной опоры
Сначала необходимо для каждого найти прогиб
на уровне
от действия только горизонтальных сил. Согласно формуле (6-175) имеем:
(1)
где — условная жесткость опоры при упругой деформации,
— начальный модуль упругости бетона при сжатии,
— приведенный момент инерции сечения опоры на уровне земли. Согласно (6-172) и (6-173) (случай сечения в форме тонкого кольца) он приближенно равен
(2)
где — толщина стенки и
-- средний диаметр кольцевого сечения опоры,
-- доля арматуры в общей площади сечения,
и
— модуль упругости арматуры (
— эквивалентная толщина стенки с учетом арматуры).
Жесткость при пластичной деформации определяется формулой (6-174)
, где
для стоек с ненапряженной арматурой и
для стоек с предварительно напряженной арматурой и ненапряженной при расчете аварийного режима,
— площадь поперечного сечения арматуры,
— радиус окружности, на которой расположены центры сечений стержней арматуры, коэффициент
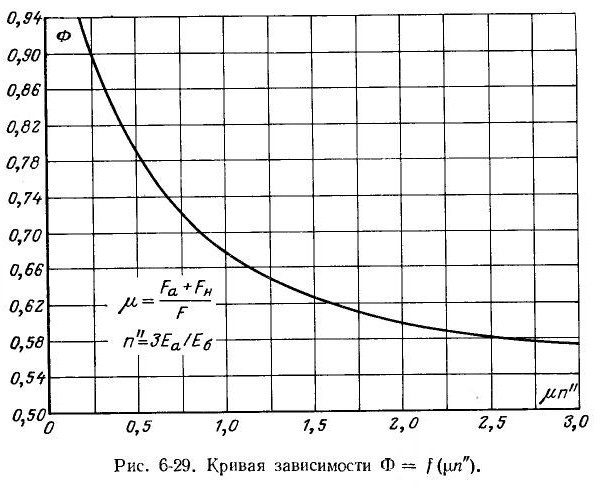
определяется по кривой на рис. 6-29 [3] (см. ниже). На этом рисунке коэффициент
равен доле арматуры в поперечном сечении стойки.
Коэффициент учитывает изгиб опоры до и после появления трещин в бетоне, так что
, где
-- изгибающий момент на уровне земли, создаваемый системой нагрузок на опору,
— часть этого момента, до которой опора работает упруго (с момента, когда изгибающий момент превысит
, упругая деформация сменится пластической с развитием трещин).
В формуле (1) , где
и
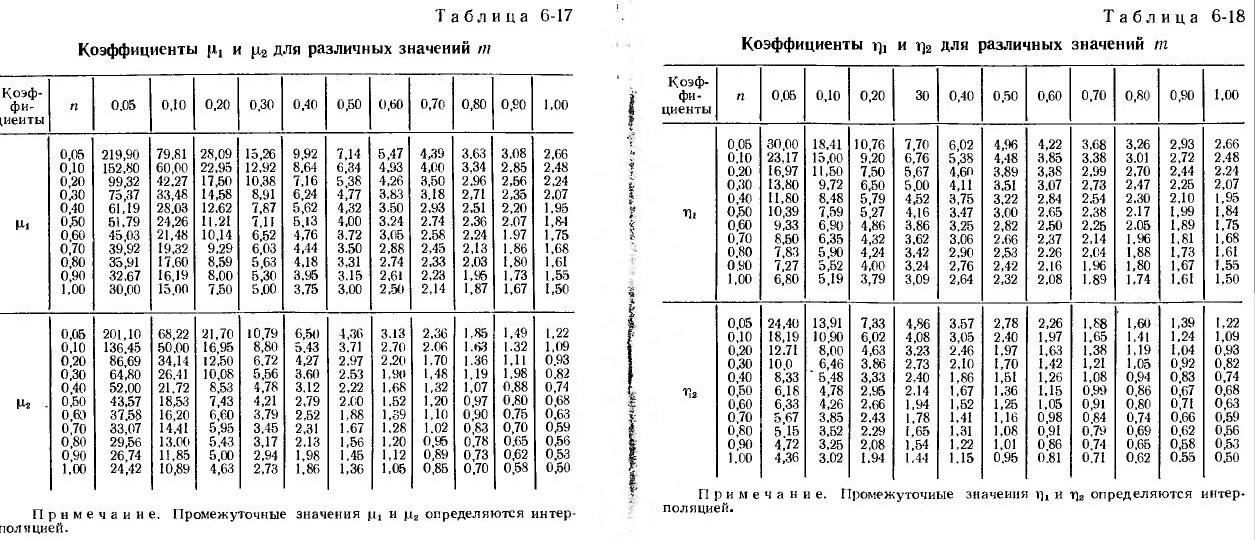
, а коэффициенты
определяются по таблицам 6-17 и 6-18 [3]. Параметр
в этих таблицах равен отношению площадей верхнего и нижнего сечений конической опоры (при
опора цилиндрическая). Аналогично, параметр
выражает изменение площади сечения арматуры по высоте опоры.
Если максимальный из прогибов превышает 1/50 высоты опоры [3], то следует принять во внимание вертикальные нагрузки. Из (6-178) получим полный прогиб
в точке
:
(3)
где приведенная (эквивалентная), вертикальная сила , эквивалентная системе сил
, и критическая сила
в силу (6-179) и (6-180) определяются по формулам:
(4)
для произвольной высоты , на которой должна находиться точка приложения силы
.
Например можно принять (так мы и сделаем). Здесь
-- прогиб на высоте
под действием единичной, горизонтальной силы, приложенной на уровне
, а
— прогиб на высоте
под действием единичной, горизонтальной силы, приложенной на уровне
, с учетом поворота опоры в грунте. В силу (6-181) имеет место выражение:
(5)
где прогибы ,
и
определяются на уровне
от единичной нагрузки, приложенной на уровне
. При этом
и
вычисляются по жесткостям
и
соответственно, а
— это прогиб, возникающий от поворота опоры в грунте, который в силу (6-182) равен:
(6)
Здесь рад. — предельно допустимый угол поворота опоры под действием наибольшего, опрокидывающего момента
[3]. Если расчет ведется для максимальной нагрузки с учетом ветра и оледенения, то
(изгибающий момент на уровне земли).
Рис. 6-29 [3]
Таблицы 6-17,6-18 [3] (следует кликнуть, чтобы рассмотреть)
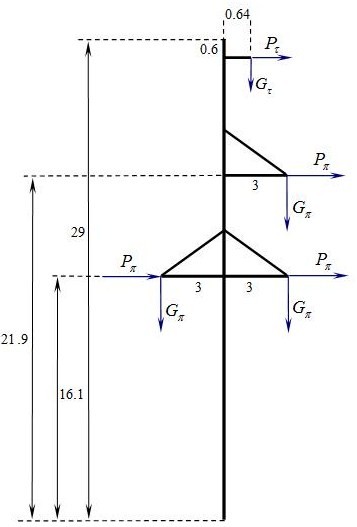 Рис. 3. Композитная опора ПК-220-1
Рис. 3. Композитная опора ПК-220-1
Расчет прогибов композитной опоры
Наша цель — применить описанную методику к расчету прогибов композитной опоры, которая подвергается распределенным ветровым и весовым нагрузкам. Предполагаем, что максимальные напряжения при изгибании опоры намного ниже предела прочности на сжатие/растяжение МПа (у стеклопластиков он близок к пределу текучести).
Заметим, что формулы (3) и (4) применимы к любой опоре, которая рассчитывается, как консоль с защемленным концом (см. (6-1) – (6-4) [3]). Поскольку композитная опора подвержена упругой деформации, в (5) следует принять , что соответствует
. Соответственно, коэффициент
не нужен, а в выражении для
вместо
следует брать модуль упругости
стеклопластикового композита, считая момент инерции
по формуле (2) в предположении
или
(оба равенства означают отсутствие арматуры и влекут
). При упругой деформации величина
равна прогибу опоры под действием единичной, горизонтальной нагрузки, приложенной на уровне
. Из (4) следует, что
(7)
Формула (1) становится неприменимой, поскольку таблицы 6-17, 6-18 [3] при отсутствии арматуры теряют смысл и не могут быть однозначно интерпретированы (не ясно, какое именно значение присвоить ). Прогибы
необходимо считать иначе. Например, с помощью интеграла Мора (5.23) [4]. Получаем следующий алгоритм.
1. Выбираем шаг дискретизации по высоте
и определяем силы
и
в точках опоры, которые находятся на уровнях
, где
и
. Например, можно принять
м.
1.1. Постоянному по высоте ветровому давлению Па на стойку соответствует система сил
, приложенных на уровнях
, где
— внешний диаметр сечения на высоте
. Для конической и цилиндрической опоры имеем
.
1.2. Собственному весу опоры (включая ледовую нагрузку на стойку) соответствует система сил
, приложенных на уровнях
, где
Н/куб.м — средний, удельный вес стойки (без учета проводов и грозозащитного троса). Можно считать, что фрагмент опоры между отметками высоты
и
представляет собой цилиндр, при этом
где объем стойки
1.3. Добавляя к этим силам ветровые и весовые
нагрузки на провода и грозозащитный трос, приложенные на некоторых уровнях
, получим полную систему горизонтальных и вертикальных сил
, действующих на опору.
Например для опоры ПК-220-1, при м, для всех
имеем
и
, при этом
,
,
,
,
,
(16.1 м и 21.9 м — уровни проводов нижнего и верхнего ярусов, 28.4 м — уровень грозозащитного троса, см. рис. 2). При этом
и
м.
2. Вычисляем прогибы от системы горизонтальных сил при всех
, действуя следующим образом.
2.1. Осевой момент инерции (кольцевого) сечения на уровне находим по формуле
, которая вытекает из (2) без арматуры.
2.2. Изгибающие моменты в точках
от системы сил
вычисляем по формуле:
2.3. Изгибающие моменты в точках
от единичной, горизонтальной силы, приложенной в точке
, определяем так:
при
и
при
.
2.4. Прогиб находим с помощью интеграла Мора (5.23) [4], который вычисляем, аппроксимируя площадью ступенчатой фигуры (учитывая, что ):
3. Вычисляем полные прогибы от системы горизонтальных и вертикальных сил, действуя следующим образом.
3.1. Для каждого находим прогиб
на уровне
под действием единичной, горизонтальной силы, приложенной на уровне
. Для этого приближенно вычисляем интеграл Мора:
3.2. Вычисляем прогиб на высоте
, с учетом поворота в грунте. Из формулы (5) при
имеем
, где
, а прогиб
определяется из формулы (6) при
и
. Момент
равен сумме моментов всех сил
относительно основания опоры, вычисляемых при максимальной, допустимой нагрузке с учетом ветра и оледенения.
3.3. По формуле (7) вычисляем приведенную силу .
3.4. По второй из формул (4) при находим критическую силу
.
3.5. По формуле (3) получаем прогибы при всех
.
4. Проверяем обоснованность предположения об упругой деформации опоры.
4.1. Вычисляем изгибающие моменты в точках
с учетом прогибов. Согласно (6-1) [3]:
(8)
где — изгибающий момент в сечении
, возникающий от эксцентриситета вертикальных нагрузок. Например, в случае опоры ПК-220-1 моменты от эксцентриситетов:
,
и
. При этом мы считаем, что на каждом уровне
приложена только одна вертикальная сила
на оси опоры, которая не может изгибать ее в недеформированном состоянии (см. п. 1.3) .
4.2. Определяем максимальные, растягивающие напряжения в сечениях на отметках высоты
. По формуле (5.3) [5] имеем
.
4.3. Проверяем условие МПа для всех
. Если оно выполняется с большим запасом, то опора работает упруго и расчет прогибов выполнен корректно. Одновременно получаем эпюру максимальных, нормальных напряжений.
Рис. 4. Траверсы композитной опоры
Практический пример
Найдем прогибы композитной опоры ПК-220-1 при типовых нагрузках, указанных производителем ЗАО «Феникс-88» [6] по нормативу для II района [1]: скорость ветра 29 м/c, давление Па. Высота опоры
м, диаметры сечений
м,
м, толщина стенки
м, модуль Юнга
ГПа, округленные нагрузки
кН,
кН,
кН,
кН,
кН (см. 1.1, 1.2, 1.3). Отсюда получаем удельный вес опоры
кН/куб.м, учитывающий веса траверс для крепления проводов.
Траверса не влияет на изгибающие моменты за исключением участка опоры длиной 2.4 м между уровням крепления подвесного и опорного изоляторов, на котором изгибающий момент от соответствующей силы равномерно спадает до нуля на уровне крепления подвеса. Очевидно, что изгибание на этом участке опоры является пренебрежимо малым. Поэтому можно считать, что нагрузки
приложены в точках подвеса проводов и грозозащитного троса. Именно так и делают обычно (см. рис. 2, 3). Принимаем значение
кНм (максимально-допустимый момент для ПК-220-1 из [6]).
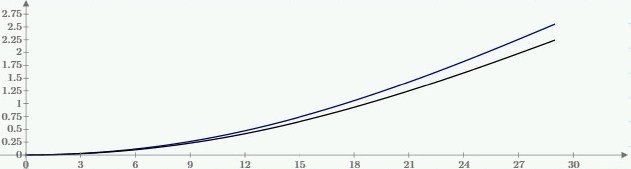
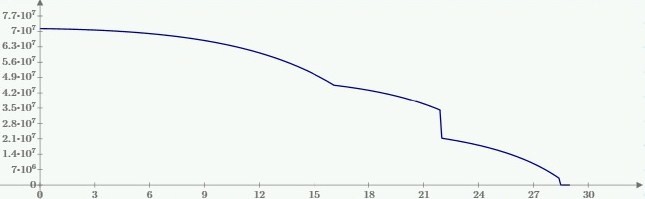
Расчет по вышеизложенной методике удобно провести в MathCad. Получаем кривые прогиба, изображенные на рис. 5. Черная кривая – прогиб от действия только горизонтальных сил, синяя кривая – прогиб с учетом горизонтальных и вертикальных сил.
Рис. 5. Прогиб опоры.
Отклонение вершины опоры (синяя кривая) = 2.56 м. При расчете только по горизонтальным нагрузкам погрешность составит 12.2%.
На рис. 6 эпюра представлена эпюра нормальных напряжений, где по вертикали отложены максимальные напряжения в МПа. Наибольшее, нормальное напряжение МПа, что примерно в 3 раза ниже предела прочности
МПа. Таким образом, опора действительно работает упруго. По формуле (8) опрокидывающий момент
кНм. Производитель указывает максимально-допустимый момент 850 кНм и коэффициент надежности 1.3 [6], поэтому опора работает в безопасном режиме.
Методика, описанная выше согласно [3], не определяет угол поворота опоры в грунте от действия горизонтальных нагрузок, хотя и учитывает возможность поворота при вычислении поправки (3) на вертикальные нагрузки. Поэтому найденные прогибы опоры ПК-220-1 слабо учитывают ее поворот в грунте, который при достижении предельного угла в 0.01 рад увеличил бы прогиб вершины на приблизительно 29 см. Соответственно, на каждом уровне прогиб
увеличился бы на
. Угол поворота опоры в грунте считается пропорциональным опрокидывающему моменту (т.е. изгибающему моменту на уровне земли), а коэффициент пропорциональности называется податливостью заделки [7]. По-видимому, она определяется опытным путем.
ЗАО «Феникс-88» предлагает эвристическую формулу для расчета опрокидывающего момента (стр. 15 [6]), которая в данном случае приобретает следующий вид:
кНм.
Этот результат отличается в 2 раза, поэтому формула ЗАО «Феникс-88» является несостоятельной. По-видимому, ее не стоит применять всерьез.
Если найти прогибы по описанной выше методике, считая ветровую нагрузку и собственный вес стойки сосредоточенными силами, приложенными на уровне [2], то погрешность прогиба стойки составит 1.2%, т.е., будет пренебрежимо малой. Погрешность эпюры напряжений более существенна, но не превышает 12.3% в центре стойки и 4.2% у основания опоры. Таким образом, эвристическая замена распределенных ветровой нагрузки и веса стойки сосредоточенными силами, которые приложены на уровне
, позволяет упростить расчеты и дает несущественную погрешность, если стойка не работает в опасной близости от предела прочности (в ураган или при большой ледовой нагрузке на провода).
Более точный расчет
В случае гибких, композитных опор формула (3), которая также принята в сопромате (8.25) [5], является грубым приближением к реальности. На самом деле игнорирование прогиба стойки от действия вертикальных сил привносит погрешность не 12.2%, а 18.6%. Если посчитать прогибы, решая уравнение упругой линии 5.21 [5]:
(9)
то получится не 2.56 м, а 2.76 м. Если же при подсчете изгибающих моментов в п. 4.1 принять во внимание радиусы опоры на уровнях траверс, добавляя их к длинам траверс (каждая по 3 м, рис. 3), то решение уравнения (9) в точке
возрастет до 2.79 м. Чтобы точней определить положение вершины опоры следует учесть сокращение ее высоты от изгибания. Для этого нужно решить уравнение
выражающее факт неизменности длины опоры при изгибании, где — высота вершины искривленной опоры. Здесь мы никак не учитываем поворот опоры в грунте, который может добавить до 29 см прогиба вершины.
С уравнением (9) не все просто — оно не является обыкновенным, дифференциальным, поскольку изгибающий момент зависит от значений искомой функции
в точках выше уровня
. Вопрос о том, как именно можно решить его, в данной статье не обсуждается. Вместо этого мы рассмотрим другой метод, описанный в 5.17.3 [7]. Он точней методики из [3] и практически не отличается по точности от метода, связанного с (9), … если прогибы опоры не имеют порядка ее размера.
Этот метод делит опору на участки с условно постоянной жесткостью
, и прогибы
определяются с помощью интеграла Мора. Поскольку изгибающие моменты зависят от прогибов, последние неявно определяются уравнением
(10)
где и
— прогиб на уровне верхней границы
— го участка,
— прогиб вершины, интегралы вычисляются по отрезкам
, момент
от нагрузки определяется в недеформированном состоянии опоры, момент
возникает от вертикальных нагрузок в результате деформации,
— изгибающий момент от единичной, горизонтальней силы, приложенной на уровне
. После аппроксимации каждого из интегралов по формуле Симпсона, момент
линейно выражается через искомые прогибы
. Уравнение (10) решается методом итераций (см. 5.17.3 [7]).
Применяя этот алгоритм к опоре ПК-220-1 получим прогиб вершины м, что на 2.5% превышает значение 2.79м, полученное из решения уравнения (9). При этом опрокидывающий момент 552 кНм на 2% превышает 540.6 кНм. Таким образом, методика из [7] дает хорошее приближение.
Как и прежде, по завершении расчета прогибов необходимо убедиться в том, что опора работает в упругом режиме (т.е., далеко от предела прочности). В данном случае это условие выполняется.
Для вычисления прогибов опор ЛЭП можно использовать метод конечных элементов (МКЭ). Существуют САПР реализующие его в инженерных расчетах (ANSYS, COSMOS и т.д.). Такие инструменты не всегда устраивают исследователей из-за закрытости по принципу «черного ящика». В случае больших прогибов следует иметь в виду, что МКЭ в принципе не обладает точностью методов, основанных на решении нелинейных уравнений (9) и (10), поскольку предполагает линейную зависимость между нагрузками и перемещениями.
ССЫЛКИ
- Правила устройства электроустановок. Утверждены Приказом № 204 Минэнерго РФ от 08.07.2002.
- Короткевич М.А., Млынчик М.И. Определение прогибов железобетонных стоек опор воздушных линий электропередачи // Энергетика. Известия высших учебных заведений и энергетических объединений СНГ. 2011. № 5. С. 11- 16. http://extremal-mechanics.org/wp-content/uploads/2017/03/LEP.pdf
- Реут М.А., Рокотян С.С. и др. Справочник по проектированию линий электропередачи. М., «Энергия». 1980. 296 с.
- Дарков А.В., Шапошников Н.Н. Строительная механика. М., «Высшая школа». 1986.
- Фесик С.П. Справочник по сопротивлению материалов. Киев: «Будiвельник». 1982.
- ЗАО «Феникс-88». Каталог продукции — композитные опоры ЛЭП // http://www.fenix88.nsk.su/files/kom_opor/opori_lep2014.pd
- Руководство по проектированию многогранных опор и фундаментов к ним для ВЛ напряжением 110-500 кВ. СТО 56947007-29.240.55.054-2010. Стандарт ОАО «ФСК ЕЭС». 2010.



Академическая версия этой статьи, дополненная алгоритмом решения уравнения (9) http://extremal-mechanics.org/wp-content/uploads/2017/06/статья-в-СМ.pdf.
Для начала было бы неплохо поинтересоваться сколько композитных опор вообще в мире установлено. Многие вопросы отпадут сразу. В России уже более миллиарда рублей сожрали. И?
Вот и поинтересуйтесь, а мне это неинтересно. Статья о другом, если вы не заметили. Чисто технические вопросы, которые она решает, не нуждаются в такого рода экономической информации.