Задача коммивояжера с возвращениями

Прямой перебор маршрутов в классической задаче коммивояжера. Источник изображения:  http://en.wikipedia.org/wiki/File:Bruteforce.gif

       Пусть проектируется сеть электроснабжения заданного набора взаимно удаленных потребителей. Примером могут служить населенные пункты одного района. Возникает задача оптимизации такой электросети по стоимости капиталовложений или потерям мощности в процессе эксплуатации. Интересно, что будущих инженеров-энергетиков не учат методам ее решения, а сами эти методы не разработаны. При выполнении дипломных проектов схему сети выбирают почти интуитивно, оценивая лишь малую часть возможных вариантов (от 2-х до 5-ти). Таким образом, задача оптимизации электросети декларируется, как цель, но фактически не решается и даже не формулируется. По-видимому, это связано с тем, что электрические сети развиваются эволюционно, следуя за новыми потребителями. Если в данный момент времени необходимо подключить новый пункт к существующей системе, то это не вызывает математических затруднений. Тем не менее, проблема выбора оптимальной сети является технически интересной и актуальной.

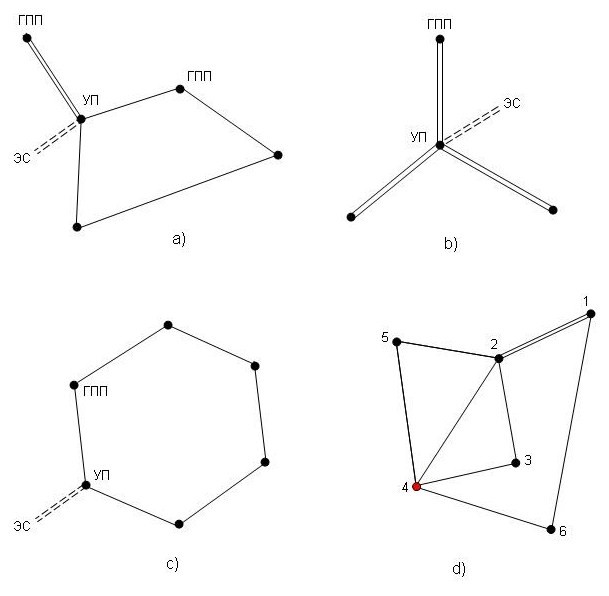
Рис. 1  Графы электросетей  

     Будем изображать сеть в виде графа, где каждое ребро отвечает одной трехфазной линии, а каждая вершина – главной понижающей подстанции (ГПП) или узловой подстанции (УП). Стандартное требование надежности состоит в том, что ГПП должна иметь два трансформатора, к которым подключены две входные (трехфазные) линии. В каждом пункте должна располагаться ГПП или УП, к последней могут быть подключены несколько ГПП. Связь между ГПП и УП также осуществляется по двойной цепи. Легко видеть, что в сетях a), b) и с) на рис. 1 обрыв любой из линий не прерывает электроснабжение каждого из пунктов.  Один пункт подключен к внешней энергосистеме (ЭС) цепью, которая на рис. 1 показана пунктиром. Пунктирные линии не входят в графы и алгоритмах не рассматриваются. Однако пункт подключения к ЭС определяет выделенную вершину графа, которая будет называться точкой старта.

      Кратность вершины – это число ребер, которым она инцидента. Например, граф а) имеет одну вершину кратности 4 и четыре вершины кратности 2 (линии подключения к ЭС в граф не входят). Каждая вершина на рис. 1 a), b) и c)  имеет четную кратность. На более низком уровне системы электроснабжения, т.е., при подключении потребителей могут возникать вершины нечетной кратности. Однако мы исходим из того, что на уровне ГПП и УП кратность вершин должна быть четной. Это соответствует инженерной практике, согласно которой в процессе формирования сети некоторые пункты соединяются по топологии кольца (рис. 1 c)), а некоторые подключаются радиально (рис. 1 b)). По соображениям надежности, каждая радиальная линия должна быть задублирована. Такими двойными цепями также могут быть связаны между собой отдельные кольца. Ниже мы уточним тип представляющего графа, а пока заметим, что он является связным и имеет вершины только четной кратности.

    Цикл удобно рассматривать, как замкнутую траекторию точки, движущейся от пункта к пункту. Поскольку каждая вершина сетевого графа имеет четную кратность, то, начав обход с любой из них, необходимо вернуться в исходной вершину. Так возникает цикл. При этом по одному ребру запрещено проходить дважды, но можно вернуться назад по второму, если данная пара вершин связана двойным ребром. Двойные ребра будем называть параллельными. Например, параллельными являются ребра между вершинами УП и ГПП на рис. 1 b). Такой путь вдоль ребер графа может не быть гамильтоновым циклом, поскольку последний не должен иметь самопересечений.

      Поскольку сетевой граф имеет выделенную вершину (точка подключения к ЭС), мы будем рассматривать только те циклы, которые начинаются и заканчиваются в этой вершине. Если такой цикл проходит через все вершины, то будем называть его маршрутом. Примеры маршрутов тривиально получаются на рис. 1 a), b), c), если начать движение с выделенной вершины и проходить по каждому ребру строго один раз, обходя вершины в любом порядке и возвращаясь в точку старта. Траекториями таких движений являются графы, а маршрутов может быть несколько. Например, на графе a) существует 8 маршрутов, а на графе с) их только 2 (по часовой стрелке и против).

    Теперь мы готовы дать определение маршрутам того типа, который рассматривается в данной статье. Пусть задан конечный набор точек, одна из которых называется точкой старта. Рассмотрим произвольный маршрут, проходящий через все эти точки, который начинается и заканчивается в точке старта. Разрешается многократно заходить в одну и ту же точку, однако эта возможность ограничена следующим требованием. Если произвольная точка пройдена более одного раза, то маршруту запрещается вторично заходить в любую другую точку, которая была пройдена между любыми двумя посещениями точки . Исключением является точка старта, в которую можно возвращаться без ограничений. Наконец, ни одно из ребер графа, представляющего маршрут, не должно соединять какую-либо вершину саму с собой (т.е., запрещено идти из точки сразу в нее же, делая петлю). Маршрут, удовлетворяющий этим условиям, называется квази-гамильтоновым.

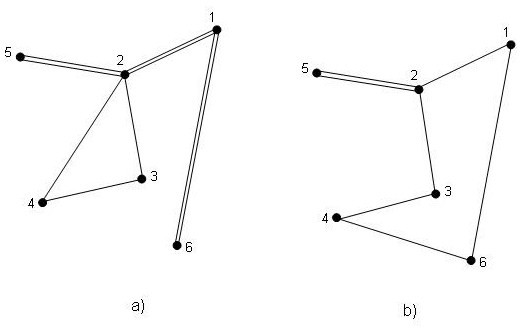
      На рис. 1 a), b) и c) таковыми являются все маршруты. Данное условие соответствует практике строительства электрических сетей. Весьма вероятно, хотя это строго не доказано, что всякий не квази-гамильтонов маршрут может быть переделан в более выгодный, квази-гамильтоновый. На рис. 1 d) маршрут 123425461 не является квази-гамильтоновым, т.к. он второй раз заходит в точку 4, ранее пройденную между двумя посещениями точки 2. На рис. 2 показаны варианты перестройки этого маршрута в квази-гамильтоновый: а)  1234252161 и b) 16432521. Если оптимизировать маршруты по длине пути, то в силу неравенства треугольника рис. 2 b) будет лучше, чем рис. 1 d), независимо от расстояний между точками.   

Рис. 2  Квази-гамильтоновы маршруты

     Заметим, что всякий гамильтонов цикл является квази-гамильтоновым маршрутом. Пусть выделенная вершина имеет номер 1. Тогда произвольный маршрут  определяется последовательностью чисел , где каждое  - номер вершины графа. Условие квази-гамильтоновости выглядит так: если любое число   встречается в этом маршруте на местах   и , так что , то ни одно из чисел последовательности  не встречается в маршруте после позиции  .

    Задача оптимизации электросети свелась к поиску оптимального квази-гамильтонова маршрута через пункты подключения, со стартовой точкой подключения к ЭС. Траекторией такого маршрута будет граф, который задает искомую конфигурацию сети. Осталось определить целевую функцию   от маршрута , которая должна быть минимизирована или максимизирована. Задав стоимость линии  между каждой парой пунктов , определим стоимость маршрута:

    где      и             (1)  

   Задача оптимизации является обобщением задачи коммивояжера и отличается только тем, что в дополнение к гамильтоновым маршрутам допускаются квази-гамильтоновые. Назовем ее задачей коммивояжера с возращениями. 

   Маршруты (циклы), которые рассматриваются в классической задаче коммивояжера, называются гамильтоновыми и характеризуются тем, что цикл заходит в каждый промежуточный пункт ровно один раз. Циклам, которые возникают в задачах оптимизации электросетей, разрешено возвращаться в одни и те же пункты, но не как попало. Квази-гамильтоновы циклы соответствуют реальным маршрутам объезда пунктов доставки, если требуется развести по ним грузы, начиная движение от склада и возвращаясь в него. При этом грузовик может проехать через ранее посещенный пункт той же самой дорогой, но в обратном направлении, если это помогает экономить время. Более того, другая дорога может оказаться недоступной. Поэтому условие задачи коммивояжера, которое исключает такого рода маршруты, выглядит чрезмерно жестким и не вполне адекватным реальности.      

     Вернемся к целевой функции задачи оптимизации электросети. Выражения (1) недостаточно, т.к. стоимость строительства сети определяется еще и тем, какого типа подстанции расположены в ее узлах при выбранном способе прокладки линий. Например, стоимость строительств УП отлична от ГПП и зависит от числа и типов трансформаторов, которые приходится использовать. Поэтому целевая функция должна зависеть не только от стоимостей ребер представляющего графа, но и от того, какое количество ребер инцидентно каждой вершине. Конкретный вид этой зависимости мы выяснять не будем. Кроме того, при оптимизации по мощности способы соединения подстанций влияют на потери при трансформации, и вид целевой функции становится еще более сложным. Однако задача коммивояжера с возвращениями имеет практическое значение не только в связи с проектированием электросетей, поэтому ограничимся целевой функцией вида (1)

      Пусть заданы набор точек (пунктов)   и  - матрица , которая определяет «стоимости» путей между пунктами, так что   - стоимость прямого пути из точки  в точку .  При   значение  не определено или считается равным . Требуется найти квази-гамильтонов маршрут   через все пункты, на котором функция (1) принимает наименьшее значение.

    В качестве дополнительного условия может быть задан граф разрешенных путей  . Его ребра соединяют пункты , между которыми «движение» разрешено. В этом случае минимум функции (1) ищется на множестве тех квази-гамильтоновых маршрутов, графы которых вложены в  без учета параллельных ребер (т.е., только одно из любой пары параллельных ребер  обязано совпадать с соответствующим ребром графа  ).  Граф   должен быть, конечно, связным и проходить через все точки  . В этом и только этом случае существует решение задачи с разрешенными путями!

      Слово «стоимость» не следует воспринимать буквально. Число может быть просто расстоянием между пунктами или иной мерой. Однако следует заметить, что если в данной задаче стоимость – не географическое расстояние и не пропорциональна ему,  то привычные свойства расстояний могут  не выполняться. Например, может не выполняться неравенство треугольника (), что совершенно естественно для электросети, оптимизируемой по расходам на строительство. Прокладка более короткой линии может обойтись дороже из-за сложностей рельефа, административных и других причин. Невыполнение неравенства треугольника влечет за собой неприменимость тех алгоритмов, которые его используют. Это относится к известному алгоритму Литтла, поэтому он не может быть адаптирован для общей задачи коммивояжера с возвращениями. Далее, поскольку стоимость прокладки двойных цепей электроснабжения может обойтись дешевле, чем двух одиночных, матрица   не обязана быть симметричной. 

    В общем случае классическая задача коммивояжера не имеет точного алгоритма, объем вычислений которого имел бы порядок  для какого-нибудь , где  - количество пунктов. Иначе говоря, точно и не слишком долго решать задачу коммивояжера невозможно. Прямой перебор маршрутов требует вычислений объемом порядка , поэтому такой метод практически неосуществим уже при  близких к 30. При это - миллиарды лет вычислений на суперкомпьютере, а при прямой перебор всех 360 гамильтоновых циклов, начинающихся в заданной точке, можно наблюдать на анимации под заголовком статьи. Последнее ребро, замыкающее цикл, там не отображается.

    Часто применяются приближенные алгоритмы, которые позволяют перестроить и этим улучшить любой исходный маршрут (методы локального оптимума). Обычно такие подходы дают хорошие результаты, хотя и не гарантируют, что полученный маршрут является оптимальным среди всех возможных. Подобным образом действуют студенты-энергетики, когда почти наугад выбирают исходный вариант сети, после чего пытаются его оптимизировать несколькими перестройками, обсчитывая варианты «вручную».

   Другой тип алгоритмов эквивалентен введению графов разрешенных маршрутов , которые неявно определяются в процессе отсечения ветвей, заведомо не ведущих к оптимальному маршруту. Таков алгоритм Литтла, который достаточно быстро и точно находит глобальное решение задачи коммивояжера (однако нуждается в неравенстве треугольника для матрицы , как было замечено).    

   В задаче коммивояжера с возвращениями также можно использовать методы локального оптимума, которые просты для реализации и достаточно эффективны. Для этого нужно построить квази-гамильтонов маршрут «на глазок», после чего начать его варьировать каким-то образом, выбрав из возникающих вариантов наилучший. Пример таких действий, предпринимаемых в классической задаче коммивояжера, описан в статье http://habrparser.blogspot.ru/2014/02/blog-post_1.html. Такой подход не гарантирует оптимальное решение, поэтому остается только верить в то, что полученное решение является достаточно хорошим. Однако при большом размере задачи, т.е. при , с этим приходится мириться.

     В этой статье представлен точный алгоритм, основанный на полном переборе квази-гамильтоновых маршрутов. XLS-файл с макросом OptimalRoute можно скачать по ссылке http://extremal-mechanics.org/?attachment_id=13093. Выбор среды VBA был обусловлен тем, что она знакома студентам ВФ МЭИ. Макрос OptimalRoute имеет интерактивный  интерфейс, поэтому пояснения о вводе исходных данных не требуются. Результат его работы — оптимальный маршрут выводится в виде последовательности пунктов, которая начинается и заканчивается точкой старта (первым из введенных пунктов).

    В задаче коммивояжера с возвращениями объем вычислений значительно больше, чем в классической задаче. Приближенная закономерность роста числа маршрутов очевидна из таблицы.

     Уже при время работы макроса на ноутбуке составило 30 минут. Та же программа в C++ будет работать значительно быстрее. Однако ясно, что практическая применимость данного алгоритма заканчивается на рубеже , а суперкомпьютеры могут добавить к  лишь несколько единиц. Для гарантированного и точного решения задачи, при матрице стоимостей без дополнительных условий, ничего лучшего пока не существует. Макрос OptimalRoute может применяться для тестирования методов локального оптимума и других приближенных алгоритмов.

   В практических приложениях естественны ограничения на разрешенные маршруты (граф ). Если ограничений много, то они могут драматически уменьшить объем вычислений. Например, в электросети района с десятками населенных пунктов, диаметрально противоположные пункты вряд ли могут быть связаны напрямую. Ограничения также возникают от ландшафта. Если рассматривать задачу коммивояжера с возвращениями, как логистическую, то все маршруты должны следовать существующим дорогам. Рассмотрим пример.

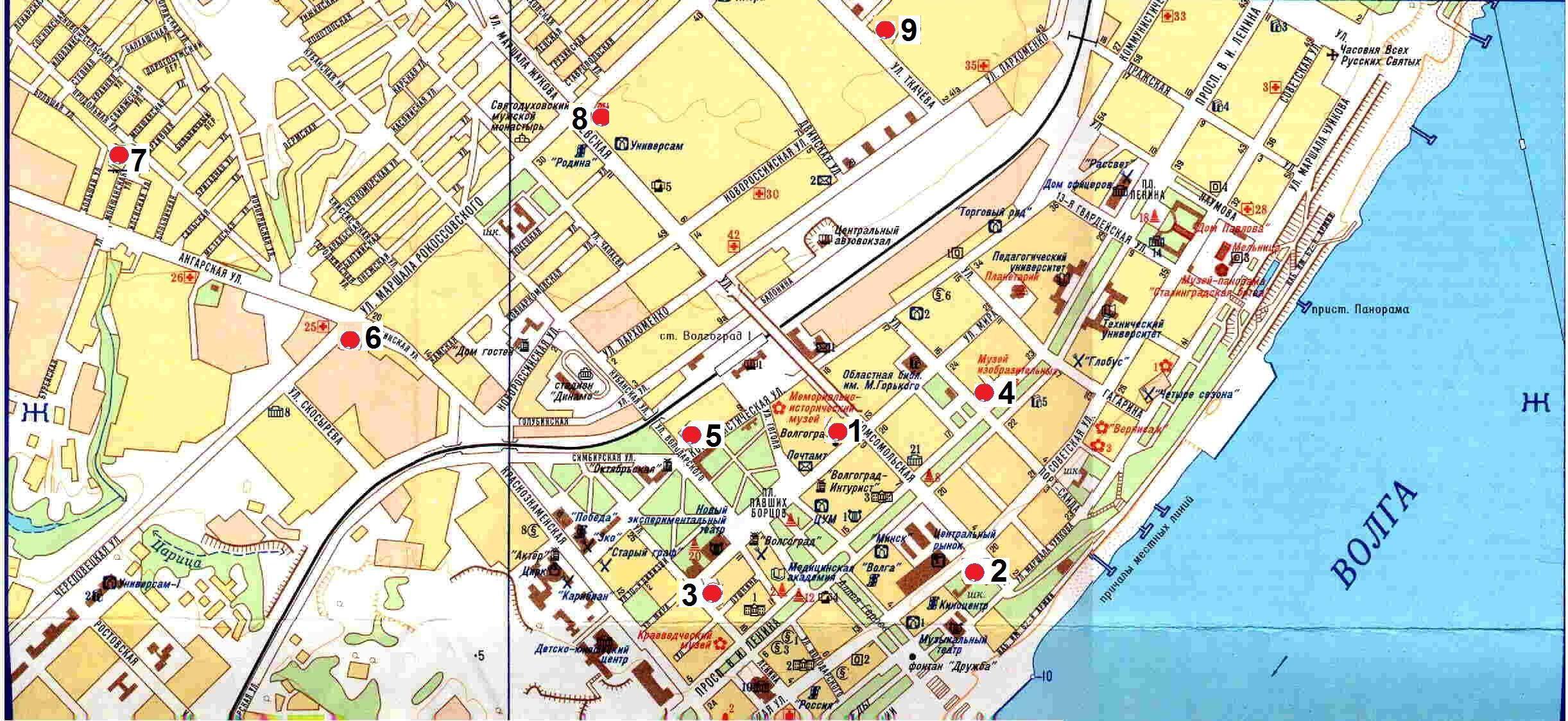
Рис. 3  Центральный район г.Волгограда

   Решается задача коммивояжера с возвращениями, где «стоимостью» является расстояние. Пункты 1 2 3 4 5 6 7 8 9 изображены на карте (рис. 3). Длины путей между ними были «на глазок» оценены в относительных единицах, поэтому не рекомендуется использовать эти входные данные. Нули соответствуют запрещенным путям. Каждый запрет связан с тем, что путь неизбежно проходит вблизи какого-то другого пункта, в силу чего прямой связи между парой пунктов нет, либо такой путь заведомо не будет выбран в реальной ситуации.