True Reverse Perspective from JMS on Vimeo.
Закон линейной перспективы устанавливает правила, следуя которым можно создать иллюзию пространственной глубины плоского изображения. По существу они сводятся к тому, что следует рисовать проекции реальных объектов на плоскость рисунка (экран) из точки, где расположен глаз наблюдателя. Кроме прямой линейной перспективы, которая также называется ренессансной, есть и т.н. обратная. Согласно правилам обратной перспективы, по мере удаления предметов их видимый размер должен увеличиваться. Такая техника характерна для Древнерусской и Византийской иконописи, и для нее находят религиозные основания. Это – как бы запечатленный образ Мира перед глазам Бога, который видит его в обычной перспективе.
В последние годы наблюдается рост интереса к данной теме. Появились, хотя пока еще редки, компьютерные программы и даже фотообъективы, которые создают изображение в обратной перспективе. Производители не раскрывают секреты таких объективов, но можно догадаться, что в них используется эффект увеличения мнимого изображения в линзе при удалении предмета и уменьшения при приближении. В данной статье обратная перспектива рассмотрена с научной точки зрения. Раскрыта ее связь с тонкой линзой. Даны формулы, посредством которых можно создавать компьютерные изображения в обратной перспективе. Все это излагается в дальнейшем. Но следующий параграф адресован тем читателям, кто хочет больше знать о прямой перспективе.
Ренессансная перспектива
Приемы перспективы были известны в Древней Греции и Риме, где использовались для рисования театральных декораций. Однако первым художником, применившим эти идеи в живописи, был Джотто ди Бондоне (1267 – 1332), хотя у него не было картин, целиком подчиненных перспективе. На рубеже XV и XVI веков закон перспективы стал общепринятым в Европе.
Фреска Джотто ди Бондоне
Закон (прямой линейной) перспективы обычно формулируется таким образом:.
- параллельные линии, удаляющиеся от наблюдателя вдаль, сближаются и сходятся в одной точке на линии горизонта (точка схода);
- одинаковые предметы и объекты при удалении от наблюдателя кажутся меньше размером и сходятся в одной точке на линии горизонта.
Здесь идет речь о предметах и линиях на рисунке, которые изображают реальные объекты и линии их контуров. Такая формулировка является неполной, поскольку точек схода может быть несколько (на этой картине как минимум еще одна — она немного выше).
«Афинская школа» (1511 г.) Рафаэль Санти
Идею ренессансной перспективы иллюстрирует гравюра Дюрера из его книги “Наставление в способах измерения” (1525 г.). На гравюре стекло, расположенное перпендикулярно лучу зрения, расчерчено на квадраты. Они помогают художнику составить целое изображение из небольших фрагментов, которые можно нарисовать «на глаз». Глядя на объект через стекло он рисует в квадратах на бумаге то, что видит в соответствующих квадратах на стекле. С помощью этой гравюры легко понять идею прямой, линейной перспективы.
Изображение на сетчатке глаза создают световые лучи, идущие от объекта. Если на их пути поставить стекло, то лучи пройдут его насквозь. Поэтому можно считать, что они исходят непосредственно от точек стекла, имеющих тот же цвет, что и лучи света, падающие на них. На месте точки стекла, на которую падает луч определенного цвета, можно нарисовать точку того же цвета. Тогда луч не пройдет через нее и рассеется, но сама эта точка испустит во все стороны пучок отраженных световых лучей того же цвета, один из которых достигнет глаза наблюдателя вместо исходного луча. Раскрасив таким образом стекло мы скроем объект от наблюдателя, а вместо этого создадим зрительную иллюзию. То, что получится на стекле, будет проекцией объекта на плоскость стекла из центра в точке, где расположен глаз. Закон линейной перспективы не касается цветности точек проекции. Для передачи расстояний цветом есть эмпирические правила «воздушной перспективы», которые мы не рассматриваем. Очевидно, что вместо стекла можно использовать бумажный лист, создав на нем точно такое же изображение.
Таким образом, чтобы создать 2-мерную иллюзию 3-мерного мира, нужно нарисовать его проекцию на плоскость из точки, в которой расположен глаз. В дальнейшем эта плоскость называется экраном, а точка положения глаза – центром перспективы. В этом и состоит точный смысл закона перспективы. Но для художника или программиста, который создает 3D изображение, нужны конкретные рекомендации. Что именно и как следует делать?
Закон прямой линейной перспективы (точная формулировка). Пусть выбраны экран изображения и неподвижная точка , соответствующая положению глаза наблюдателя. Тогда любой пучок параллельных линий, являющихся краями реальных объектов и не параллельных экрану, изображается на нем пучком лучей, имеющих общую вершину. Эту вершину, называемую точкой схода, дает пересечение с плоскостью экрана луча зрения, который исходит из
параллельно линиям пучка. Пусть любой отрезок, являющийся ребром реального объекта, смещается в произвольном направлении, так что в начальном и конечном положении отрезок параллелен экрану, и его длина не меняется. Тогда размер изображения отрезка обратно пропорционален его удаленности от плоскости, которая проходит через точку
параллельно экрану.
Геометрические подробности и доказательства собраны здесь http://extremal-mechanics.org/wp-content/uploads/2014/01/ренессансная-перспектива..pdf. Следует заметить, что если отрезок не параллелен плоскости экрана, то изменение его видимых размеров не подчиняется закону обратной пропорциональности. Если расстояние от центра перспективы до экрана намного меньше расстояний до изображаемых предметов, т.е.
, то видимые размеры параллельных экрану отрезков можно считать обратно пропорциональными их удаленности от плоскости экрана.
Как видно из рисунка, точки схода (здесь их 6) не обязаны лежать на линии горизонта и самого горизонта может не быть. При фиксированных центре перспективы и луче зрения (направлении взгляда), точка схода будет одна. Она получается на пересечении луча зрения с плоскостью экрана. Но в процессе рассматривания объекта меняется направление взгляда и положение глаза, и каждому такому изменению может соответствовать новая точка схода. Не стоит также забывать, что левому и правому глазам соответствуют разные точки схода.
При этом картина может быть подчинена т.н. перспективному единству, а может быть и не подчинена ему. В первом случае художник рисует так, как если бы он видел мир одним глазом (допустим правым), положение которого не изменяется. Тогда однозначно определена проекция на плоскость рисунка (экран), но точек схода может быть несколько — в зависимости от направлений реальных параллельных линий. Отсутствие перспективного единства означает, что в процессе рисования художник по своему усмотрению меняет положение глаза. Соответственно меняется и проекция, поэтому, по существу, изображение склеивается из реалистичных фрагментов. Это — обычная практика, хотя не соблюдая перспективное единство художник отходит от задачи реалистичного изображения. Однако фотография всегда подчинена перспективному единству, т.к. в момент снимка центром проекции является центр входного отверстия объектива (диафрагмы).
Еще одно замечание касается понятия горизонта. В традиционных формулировках закона перспективы ему уделяется важное значение, хотя, на самом деле, линия горизонта не является чем-то важным для построения перспективного изображения. В городском или горном пейзаже, например, ее может не быть. Просто края дорог, домов и других построек всегда параллельны поверхности Земли, «бесконечно удаленная» часть которой проектируется на видимый горизонт. Так возникает линия горизонта на экране, в точках которой сходятся края дорог, уходящие вглубь ребра домов и т.п.. Если поверхность Земли (или моря) не присутствует на картине, то линия горизонта не нужна совсем.
Картина Дика Термеса (2006) на сфере с 30-ю точками схода http://termespheres.com/about-dick-termes/
Обратная перспектива
В Древнерусской и Византийской иконописи использовался прием обратной перспективы вместо ренессансной. Согласно этим правилам, по мере удаления предметов их видимый размер должен увеличиваться. Точек схода и линии горизонта здесь быть не может, т.к. бесконечно удаленные предметы были бы бесконечно большими. Известный православный философ П.А. Флоренский (1882-1937) в статье http://philologos.narod.ru/florensky/fl_persp.htm анализирует и критикует ренессансную перспективу, как омертвляющий духовное содержание прием, который сковывает творческую инициативу художника жесткими требованиями перспективного единства. С самого Возрождения художники свободно отступают от него, исходя из разных творческих соображений. Но если художник хочет создать реалистичный образ пространства в целом, то он должен следовать ренессансной перспективе с фиксированным центром (перспективное единство).
Икона XVI века, изображение в обратной перспективе
Если принять во внимание психофизические особенности работы глаз и мозга, то выяснится, что прямая перспектива создает искажения. Они особенно сильны для не протяженных предметов, близко расположенных к экрану. Поэтому художники используют аксонометрию, т.е., параллельную проекцию на экран вдоль луча зрения, когда рисуют близкие предметы. В аксонометрии видимые размеры при удалении/приближении объекта не меняются.
Как отмечали П.А. Флоренский и Б.В. Раушенбах, иногда люди видят близкие предметы в обратной перспективе (Раушенбах Б.В., «Системы перспективы в изобразительном искусстве»). Академик Раушенбах установил, что видимый угол расхождения параллельных линий не превышает 10 градусов. Обратная перспектива возникает также вследствие психологического механизма константности формы. Мозг старается построить образ объекта так, как он должен выглядеть, исходя из жизненного опыта и игнорируя искажения зрительного образа на сетчатке. Раушенбах объяснил, что из-за действия данного механизма человек иногда видит близкие предметы так, как нарисовать невозможно, а при попытке изобразить получается рисунок в обратной перспективе. При этом она может быть не слабой, т.е., с «расхождением» параллельных больше 10 градусов.
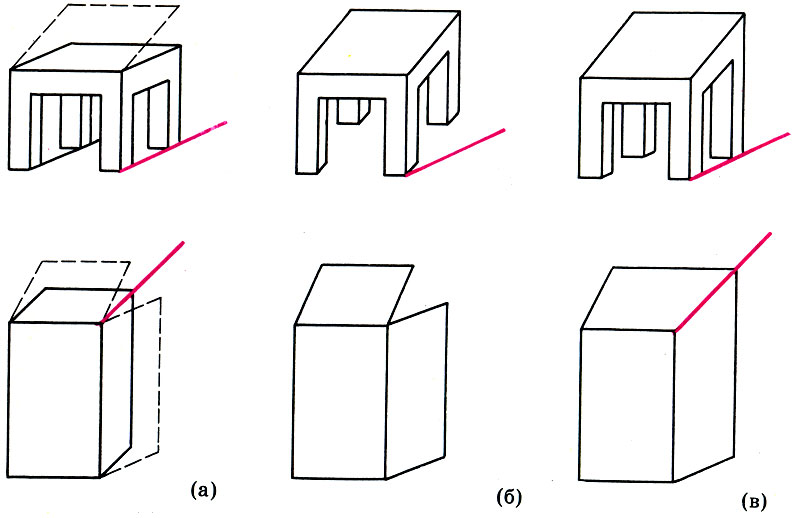
Чертеж объясняет данный эффект. На рис. а) изображены объекты в аксонометрической проекции, а пунктиром показаны образы реальных прямоугольников, которые воссоздает мозг, исходя из знания о внешнем виде прямоугольников и пытаясь приблизить их образы к прямоугольникам. Фактически возникает иллюзия! При этом получаются менее узкие параллелограммы, а все остальные части предметов мозг видит так, как они отображаются на клетчатке глаза, т.е., почти в аксонометрии. Получаются перцептивные образы, при попытке изобразить которые получится рис. б). Красные линии отвечают на картине реальным прямым, вдоль которых располагаются уходящие в глубину ребра. Чувствуя и желая исправить это противоречие, художник искажает рисунок — в). Так возникает сильный эффект обратной перспективы для отдельно взятых предметов (например, массивное Евангелие на иконах).
Таким образом, кроме религиозной, обратная перспектива имеет под собой научную основу. Но зрительное восприятие в обратной перспективе является локальным и никогда не распространяется на все видимое пространство. Кроме того это — слабый эффект. Механизм константности формы также является локальным. Он иногда порождает нечто похожее на обратную перспективу, но в общем ей не подчиняется. Поэтому возникает следующий вопрос. Имеет ли под собой физическую основу сильная обратная перспектива всего пространства или его ближней части ?
В старину окна домов обычно были непрозрачными (слюдяные окна), а люди были любопытными всегда и потому, вероятно, смотрели с улицы в окна (телевизоров еще не было). Если в глубине дома горела свеча, лучина или лампадка, то на окне отображались тени людей, как кадры кино на экране. Когда человек приближался к окну из глубины дома, размер его силуэта уменьшался, а когда удалялся – увеличивался. Отсюда один шаг до мысленного образа Бога, который освещает своим светом Мир во мраке, так что вещи и люди в нем видны, как на экране. Возможно, что именно так возникла идея обратной перспективы для икон.
Это соображение подсказывает точное определение обратной перспективы. По аналогии с прямой перспективой обратная – это проекция реального пространства на экран. Но центр проекции должен был другим. Про него часто пишут, что он находится где-то внутри наблюдателя. Однако тогда при приближении объекта к наблюдателю размер его проекции увеличивался бы, а при удалении — уменьшался. Этого не должно быть при обратной перспективе, поэтому ее центр находится по другую сторону экрана.
Определение. Обратной перспективой называется проекция на экран из центра , который располагается по другую сторону экрана от наблюдателя. При этом проектируемые фигуры должны располагаться между экраном и параллельной ему плоскостью, проходящей через точку
(т.н. фокальной плоскостью).
Пусть точка лежит на положительной полуоси
на расстоянии
от начала координат. Тогда для любой точки
ее проекция из центра
на плоскость
имеет координаты
, которые выражаются следующими формулами:
С помощью этих формул можно строить компьютерные изображения и анимацию в обратной перспективе. Однако следует иметь ввиду, что и при
изображение размывается.
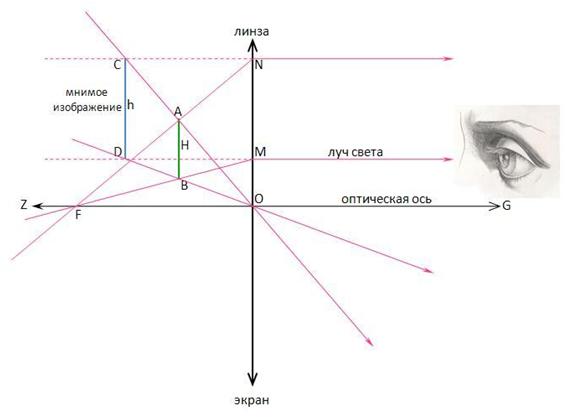
Эффект увеличения изображения при удалении предмета и уменьшения при приближении наблюдается в линзе. Это дает ключ к пониманию физической природы обратной перспективы. При этом собирающая линза создает мнимое изображение предмета, которое можно увидеть человеческим глазом. Хрусталик соберет в точку на клетчатке каждый пучок лучей, имеющих мнимый центр в точке мнимого изображения. Все остальное сделает мозг, так что в итоге мнимый образ станет видимым, как если бы на его месте находился сам объект (в увеличенном или уменьшенном размере). Можно проверить, что только мнимое изображение в собирающей линзе ведет себя согласно обратной перспективе. Поэтому наблюдаемые объекты должны располагаться между линзой и ее фокальной плоскостью. При приближении к ней мнимое изображение удаляется в бесконечность, и его размер стремится к бесконечности. Чтобы наблюдать этот мнимый образ пространства, наши глаза должны располагаться по другую сторону линзы. То, что мы при этом увидим будет ничем иным, как аксонометрической проекцией мнимого изображения на главную плоскость линзы. На рисунке такой мнимый образ СD реального отрезка AB проектируется на видимый отрезок NM.
Теорема 1. Обратная перспектива является композицией аксонометрии вдоль оптической оси тонкой, собирающей линзы на ее главную плоскость и мнимого отображения в этой линзе. При этом фокус линзы является центром перспективы , а главная плоскость линзы совпадает с плоскостью экрана.
Доказательство мгновенно следует из способа построения мнимого изображения. Эта теорема математически точно выражает связь между обратной перспективой и линзой. Рассматривается идеальная линза, которая имеет достаточно большой размер, чтобы в ней можно было видеть все, что требуется изобразить в обратной перспективе. С помощью такой линзы можно придать больше ясности мистическим представлениям о Боге, который видит Мир в обратной перспективе. А именно, Бог смотрит на нас через гигантскую линзу с большим фокусным расстоянием. То, что он при этом наблюдает, подчинено закону обратной перспективы.
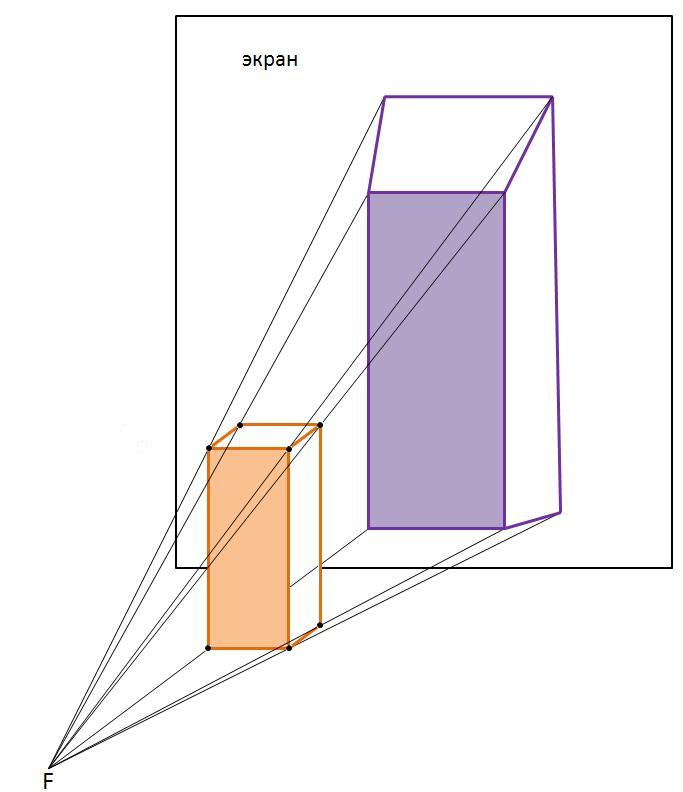
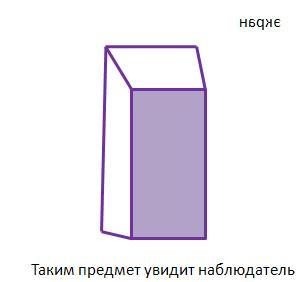
Закон обратной перспективы. Пусть заданы экран и центр перспективы . Тогда любой набор параллельных линий изображается отрезками, продолжения которых сходятся в одной точке. Она является точкой пересечения с экраном прямой, проходящей через
параллельно линиям набора. Видимый размер любой линии, параллельной экрану и имеющей неизменную длину, обратно пропорционален ее расстоянию от фокальной плоскости.
Зависимость видимого размера отрезка (параллельного экрану) от расстояния до фокальной плоскости выглядит также, как в случае прямой перспективы. Однако в обратной перспективе фокус и точка наблюдения находятся по разные стороны экрана. Поэтому, по мере приближения отрезка к фокальной плоскости, он удаляется от экрана и наблюдателя. При этом его видимый размер увеличивается, а при прямой перспективе он бы уменьшался.
Заметим, что в обратной перспективе можно отобразить лишь ту часть пространства, которая расположена между экраном и фокальной плоскостью. По мере приближения объекта к ней размер изображения стремится к бесконечности. Теперь мы можем объяснить, почему объектив обратной перспективы Elite Reverse Perspective Lens имеет максимальную дистанцию съемки 750 мм. Все дело в том, что фокусное расстояние «внешнего» объектива немногим больше 750 мм. Есть еще «внутренний» объектив, который преобразует мнимое изображение «внешнего» объектива в действительное изображение на фотопленке. Это похоже на то, как глаз человека работает в паре с линзой (см. чертеж выше).
Таким образом, в обратной перспективе нет никакой мистической тайны. Это лишь то, что мы могли бы увидеть в линзе с достаточно большим фокусным расстоянием. Хотя наблюдать мир сквозь маленькую линзу невозможно — слишком мало света от каждого предмета попадет в нее. Кроме того большое фокусное расстояние, которое измеряется сотнями метров, практически невозможно обеспечить из-за погрешностей изготовления малой линзы. Сделать огромную линзу также очень сложно (хотя их делают для больших телескопов, но с малым фокусным расстоянием). Поэтому «фотографии в обратной перспективе», которые изображают большие куски пространства, являются лишь имитациями http://www.photodom.com/ru/photo/1776649.

Объектив обратной перспективы (это не реклама)
Однако, вероятно можно использовать объектив обратной перспективы в паре с телескопом, который создаст действительное изображение удаленных предметов в зоне между обратным объективом и его фокальной плоскостью. Насколько успешными будут такие эксперименты — покажет только опыт. С практической точки зрения возможность разглядывать в увеличении детали удаленных объектов может оказаться интересной.
Следует заметить, что иногда обратной перспективой называют оптические иллюзии, которые не имеют к ней никакого отношения. Примером служит творчество Patrcik Huges http://www.patrickhughes.co.uk/.
В заключение дана не столь очевидная теорема об «обратной связи» между линзой и обратной перспективой. Грубо говоря собирающая линза — это такой оптический прибор, который дает мнимое изображение близких предметов в обратной перспективе. Обе теоремы, по-видимому, являются новыми результатами.
Теорема 2. Пусть некоторая оптическая система (объектив) имеет ось симметрии , на которой фиксированы точка
(т.н. оптический центр) и пара точек
(т.н. фокусы), равноудаленных от
на некоторое расстояние
. Назовем плоскости
и
, которые перпендикулярны оси
, главной и фокальной соответственно, где
. При любом
предположим, что каждая точка
, лежащая между главной и фокальной плоскостью
, мнимо отображается в точку
луча
. Это означает, что в
сходятся обратные продолжения лучей на выходе из объектива, в которые преобразовались световые лучи, испущенные точкой
. Предположим также, что при аксонометрии любого мнимого образа на плоскость
вдоль оси
получится изображение в обратной перспективе c центром в том фокусе
, со стороны которого расположен отображаемый объект. Тогда эта оптическая система является идеальной тонкой линзой с оптическим центром
, главной оптической осью
, фокусами
и фокусным расстоянием
.
Доказательство. Пусть координатные оси лежат в плоскости
, началом отсчета является точка
и ось
совпадает с
. Рассмотрим пучок входящих со стороны фокуса
лучей, которые параллельны вектору
. Пусть некоторый луч пучка лежит на прямой
. Произвольная точка
лежит на каком-то луче
данного пучка, а ее мнимым изображением является
. Обратное продолжение луча
, который получается из
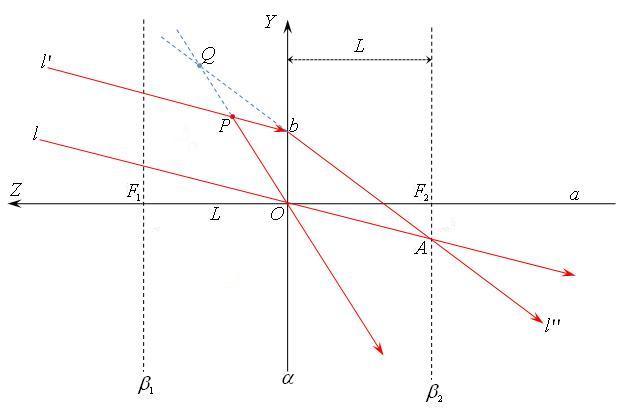
на выходе из объектива, показано голубым пунктиром.
Рассмотрим ортогональную проекцию этой конфигурации на плоскость (изображено на рисунке). Проекции всех линий и точек сохраняют исходные обозначения. Прямая
имеет уравнение
, где
Поскольку
и отображение
является обратной перспективой с центром
, то :
Отсюда следует, что . Это — уравнение прямой
. Подставляя в него
получим
, где
. В этой точке прямая
(с уравнением
) пересекает проекцию плоскости
на
. Аналогично можно доказать, что ортогональная проекция луча
на плоскость
пересекает проекцию плоскости
в точке
, где
.
Возвращаясь в 3-мерное пространство видим, что пересекает фокальную плоскость
в точке
. В силу произвольности луча
из данного пучка доказано фокальное свойство собирающей, тонкой линзы. Этим завершается доказательство теоремы.
Дмитрий Зотьев









Мне приятно, что эта статья вызывает значительный интерес, судя по числу просмотров. Без ложной скромности, она того заслуживает ))
Благодарю за статью. Таня
И Вам спасибо на добром слове ))
Спасибо. Очень хорошая статья.
Спасибо за Ваш отзыв ))
Спасибо за статью, очень интересно!
Спасибо за Вашу оценку ))
Иногда уже решенная задача является только исходными данными для следующей. Красиво написано, душевно. Отдохнул читая.
Cпасибо ))
Очень интересно, спасибо
Спасибо за интерес к моей статье! Она заслуживает этого, без ложной скромности ))
Спасибо! Можно ли с Вами связаться?
очень классная статья) Спасибо!
Вам спасибо за добрые слова! ))
Крутецки
Не могу найти ответ на вопрос об проблеме геометрической перспективы в декорации 16века.
как быть?
Извините, у меня не было намерения Вас ничем задеть. Однако, как человек, некогда профессионально занимавшийся композицией и проектированием оптических систем, я заметил неточности. Долго колебался и решил все-таки написать.
Теперь мои комментарии, на Ваши возражения:
1. В формулировке Теоремы 1 есть: «При этом фокус линзы является центром перспективы F, а главная плоскость линзы совпадает с плоскостью экрана.»
Да, «центр перспективы» я заменил на «центр проекции», так как центр проекции будет правильней.
2-3. Ход мыслей такой:
а) Все лучи света, которые формируют изображение на сетчатке наблюдателя (или на матрице фотоаппарата) проходят через зрачок глаза (или диафрагму объектива). Другие лучи участия в формировании изображения не принимают.
б) Если мы выполним обратную трассировку веера лучей от зрачка в сторону линзы, то эти лучи снова соберутся по другую её сторону. И «создадут» изображение зрачка. В оптике это называется входным зрачком всей оптической системы (глаз + тонкая линза).
в) Т.е. чисто формально тонкая линза создаёт входной зрачок позади рассматриваемых предметов. И именно через этот зрачок мы как бы «смотрим» на мир. И это развитый приём или формализм, которым пользуются оптики.
г) Как можно заметить, положение входного зрачка будет зависеть от расположения глаза наблюдателя:
- Разместив глаз вплотную к линзе, входной зрачок совпадет со зрачком глаза, и никакой обратной перспективы мы не увидим. Мы просто наденем очки с плюсовыми диоптриями.
- Чтобы увидеть обратную перспективу, глаз должен располагаться на расстоянии не менее фокусного от линзы.
- На расстоянии равном фокусному мы увидим аксонометрическую проекцию.
- Разместив глаз на расстоянии равном двойному фокусному, входной зрачок также будет располагаться на двойном фокусном расстоянии по другую сторону линзы. Предметы можно располагать на расстоянии вплоть до двойного фокусного от линзы.
Если у Вас есть интерес, то я бы мог доработать концовку статьи. На соавторство не претендую. Согласие на использование материала тоже дам.
Еще бы времени на это найти.
Да нет никакой обиды )) Просто мне показалось, что Вы — самоуверенный дилетант, с которым не о чем говорить. Возможно я ошибся. Сейчас мне некогда, позднее вникну в Ваш комментарий по существу.